3 効果量

前章では、 R の世界に慣れ親しみ、データのインポートと操作に役立ついくつかのツールを学んだ。本書の第 2 部では、 R の知識を応用して拡張しながら、メタ分析で使用される主要な統計技術について学習していこう。

Chapter 1.1 では、メタ分析を「複数の研究から得られた定量的な結果を要約する手法」と定義した。メタ分析では、個人ではなく研究が分析の基本単位となる。

これは新たな問題を引き起こす。一次研究において、収集したデータを記述するための要約統計を計算することは、通常、非常に簡単である。例えば一次研究では、連続変数アウトカムの算術平均 (arithmetic mean) $\bar{x}$ と標準偏差 (standard deviation) $s$ を計算するのは、非常によくある手法である。

しかし、これが可能なのは、通常、一次研究において本質的な前提条件の一つが満たされているからである。この条件とは、アウトカム変数がすべての研究対象者において同じ方法で測定されたことである。メタ分析では、この前提は通常満たされていない。中学校 2 年の数学能力をアウトカムとするメタ分析を実施したいと想像してみよう。どんなに厳密な包括基準を適用しても (Chapter 1.4.1 参照)、すべての研究がまったく同じテストを使って数学能力を測定しているとは思われないし、テストの合格・不合格の割合だけを報告している研究もあるかもしれない。このため、アウトカムを直接定量的に統合することは事実上不可能である。

メタ分析を行うには、すべての研究にわたって要約される効果量 (effect size) を見つけなければならない。そのような効果量は、論文から直接抽出できることもあるが、多くの場合、研究で報告された他のデータから計算する必要がある。効果量の計量は、メタ分析の結果およびその解釈可能性に大きな影響を与える可能性がある。そのため、重要な基準を満たす必要がある (Lipsey and Wilson 2001; Julian Higgins et al. 2019)。特に、メタ分析で選択される効果量指標は、以下のようなものであるべきである。

比較できる (Comparable). 効果量の測定は、すべての研究において同じ意味を持つことが重要である。再び数学のスキルを例にとってみよう。異なるテストを使用した研究において、数学のテストで達成した点数における実験群と対照群の差をプールすることは意味がない。例えば、テストは難易度や達成できる最大点数が異なる場合がある。
計算できる (Computable). 効果量の指標は、主要な研究からその数値を導き出すことが可能である場合のみ、メタ分析に使用することが可能である。含まれるすべての研究のデータに基づいて、効果量を計算することが可能でなければならない。
信頼できる (Reliable). たとえ含まれるすべての研究の効果量を計算できたとしても、それらを統計的にプールすることもできなければならない。メタ分析で何らかの指標を用いるには、少なくとも標準誤差 (次章参照) を算出できなければならない。また、効果量の形式が、適用したいメタ分析手法に適しており、推定値に誤差やバイアスが生じないことも重要である。
解釈できる (Interpretable). 効果量の種類は、リサーチクエスチョンに答えるために適切でなければならない。例えば、2つの連続変数間の関連性の強さに関心がある場合、効果の大きさを表すには相関を用いるのが一般的である。相関の大きさを解釈するのは比較的簡単で、多くの研究者が理解することが可能である。しかし、この後の章では、解釈しやすく、かつ統計計算に最適な結果指標を用いることができない場合があることを学びる。このような場合、効果量をプールする前に、より良い数学的特性を持つ形式に変換する必要がある。

「効果量」という言葉は、すでにどこかで目にしたことがあるのではないだろうか。私たちも、この言葉が何を表しているのか、あまり気にせずに使ってきた。そこで、次節では、「効果量」という言葉が実際に何を意味しているのかを探ってみたい。

3.1 効果量とは何か？

効果量とは、本書では 2 つの実体の間の関係を定量化する指標と定義する。効果量は、この関係の方向と大きさを捉えたものである。関係性が同じ効果量として表現されていれば、それらを比較することが可能である。

ここで強調したいのは、これは効果量の意味を定義するための1つの方法に過ぎないということである。効果量の定義には幅があり、人によって使い方が異なる (Borenstein et al. 2011, chap. 3)。研究者の中には、介入研究の結果に言及する際にのみ効果量を定義する人もおり、治療群と対照群の差として表現される (Chapter 3.3.1 参照)。この概念では、「効果量」とは、ある治療の効果とその大きさを指す。

私たち、これはかなり狭い定義であると考えている。治療が何らかの変数に影響を与えるだけでなく、人間が直接介入しなくても、効果は自然に現れることもある。例えば、親の収入や親の教育などの社会人口統計学的変数が、その子どもの教育達成度に影響を与える可能性がある。相関は、ある変数の値から別の変数の値をどれだけ予測できるかを記述し、効果量の一形態として見ることもできる。

逆に、メタ分析としてプールできるものはすべて自動的に効果量になる、というのは行き過ぎかもしれない。これから学ぶように、サンプル平均のような中心傾向 (central tendency) の指標はメタ分析に用いることが可能だが、これだけでは 2 つの現象の関係を定量化することはできず、「効果」は存在しない。とはいえ、本書では、実際の効果の推定値だけでなく、「一変数」や「中心傾向」の指標も表す、全体を代表する部分 (pars pro toto) として、「効果量」という言葉をよく使う。これは正確だからではなく、その方が便利だからである。

「効果量」という言葉を全面的に否定する人もいる。その主張は、「効果量」の「効果」という言葉が、因果関係を示唆していると強調しているためである。しかし、私たちは皆、相関は因果関係ではないことを知っており、介入群と対照群の差が自動的に治療そのものを原因とするものであってはならない。最終的にどちらの定義を好むかは使う人次第であるが、効果量について話すとき、人々は異なる概念を持っているかもしれないことを意識する必要がある。

数学の表記法では、真の効果量を表す記号としてギリシャ文字のシータ ($\theta$) を用いるのが一般的である⁸。より正確には、 $\theta_k$ は研究 $k$ の真の効果量を表している。真の効果量は、公表された研究アウトカムに見られる観察された効果量と同一ではないという点は重要である。観測された効果量は、真の効果量の推定値に過ぎない。私たちが言及する実体が推定値に過ぎないことを明確にするために、ハット (^) の記号を使用するのが一般的である。したがって、真の効果量の推定値である $k$ 試験で観測された効果量は、$\hat\theta_k$ (「シータ・ハット・k」と読む) と書くことが可能となる。

しかし、なぜ $\hat\theta_k$ と $\theta_k$ は異なるのだろうか？それは、サンプル誤差のためで、 $\epsilon_k$ (「イプシロン・k」と読む) として記号化できる。どのような一次調査でも、研究者は母集団全体から小さなサンプルしか抽出することができない。例えば、プライマリケア患者の心臓血管の健康に対する定期的な運動の効果を調べたい場合、世界中のプライマリケア患者すべてではなく、ごく一部の患者を対象とすることが可能である。無限に大きな母集団から小さなサンプルしか取れないということは、観察された効果が真の母集団効果とは異なることを意味する。

つまり、 $\hat\theta_k$ は $\theta_k$ にサンプル誤差 $\epsilon_k$ を加えたものと同じになる⁹。

\[\begin{align} \hat\theta_k = \theta_k + \epsilon_k \tag{3.1} \end{align}\]

研究 $k$ の効果量推定値 $\hat\theta_k$ が真の効果量にできるだけ近く、かつ $\epsilon_k$ が最小であることが望ましいのは明らかである。すべての条件が同じであれば、$\epsilon$ が小さい研究ほど、真の効果量の正確な推定値を提供すると考えることが可能である。メタ分析の手法では、効果量の推定値の精度を考慮する (Chapter 4 参照)。異なる研究の結果をプールする場合、精度が高い (サンプル誤差が少ない) 効果ほど、真の効果量の推定精度が高いため、高いウェイトを与える (L. Hedges and Olkin 2014)。

しかし、サンプル誤差の大きさはどのようにして知ることができるのだろうか。当然のことながら、研究の真の効果は $\theta_k$ なので、$\epsilon_k$ も不明である。しかし、多くの場合、統計理論を使ってサンプル誤差を近似的に求めることが可能である。一般に、$\epsilon$ を定量化する方法として、標準誤差 ($SE$) がある。標準誤差は、サンプル分布の標準偏差として定義される。サンプル分布とは、母集団から同じサンプルサイズ $n$ のサンプルを多数回無作為に抽出したときに得られる指標の分布のことである。

R でデータをシミュレートすることによって、これをより具体的に見てみよう。rnorm 関数を使って、より大きな母集団から無作為にサンプルを抽出しているようにしてみたい。この関数名は、正規 (normal) 分布から無作為 (random) サンプルを作成することからきている。rnorm 関数は、真の母集団で値がどのように分布しているかを知っているという「完璧な世界」をシミュレートし、サンプルを取ることを可能にする。

この関数は、以下の3つの引数を取る。すなわち、n: サンプルとして取得したい観測数、mean: 母集団の真の平均値、sd: 真の標準偏差である。rnorm 関数は乱数要素を持っているので、結果を再現するために、まず seed を設定する必要がある。これは set.seed 関数で行うことができるが、数値を指定する必要がある。この例では、123 を seed に設定する。さらに、母集団の真の平均は $\mu =$ 10、真の標準偏差は $\sigma =$ 2、サンプルは $n=$ 50のランダムに選んだ観測からなり、これを sample という名前で保存するシミュレーションをしたい。

このようなコードになる。

set.seed(123)
sample <- rnorm(n = 50, mean = 10, sd = 2)

さて、サンプルの平均を計算することが可能である。

mean(sample)

## [1] 10.06881

平均は $\bar{x} =$ 10.07 であり、すでに母集団における真の値に非常に近いことがわかる。ここでやったことを繰り返すと、サンプル分布ができあがる。このプロセスをシミュレートするために、先ほどのステップを 1000 回実行する。

その結果を Figure 3.1 のヒストグラムに示す。サンプルの平均は、平均が 10 の正規分布に近いことがわかる。さらに多くのサンプルを抽出すれば、平均の分布はさらに正規分布に近くなる。この考え方は、統計学の最も基本的な考え方の1つである「中心極限定理」(central limit theorem) で表現されている (Aronow and Miller 2019, chap. 3.2.4)。

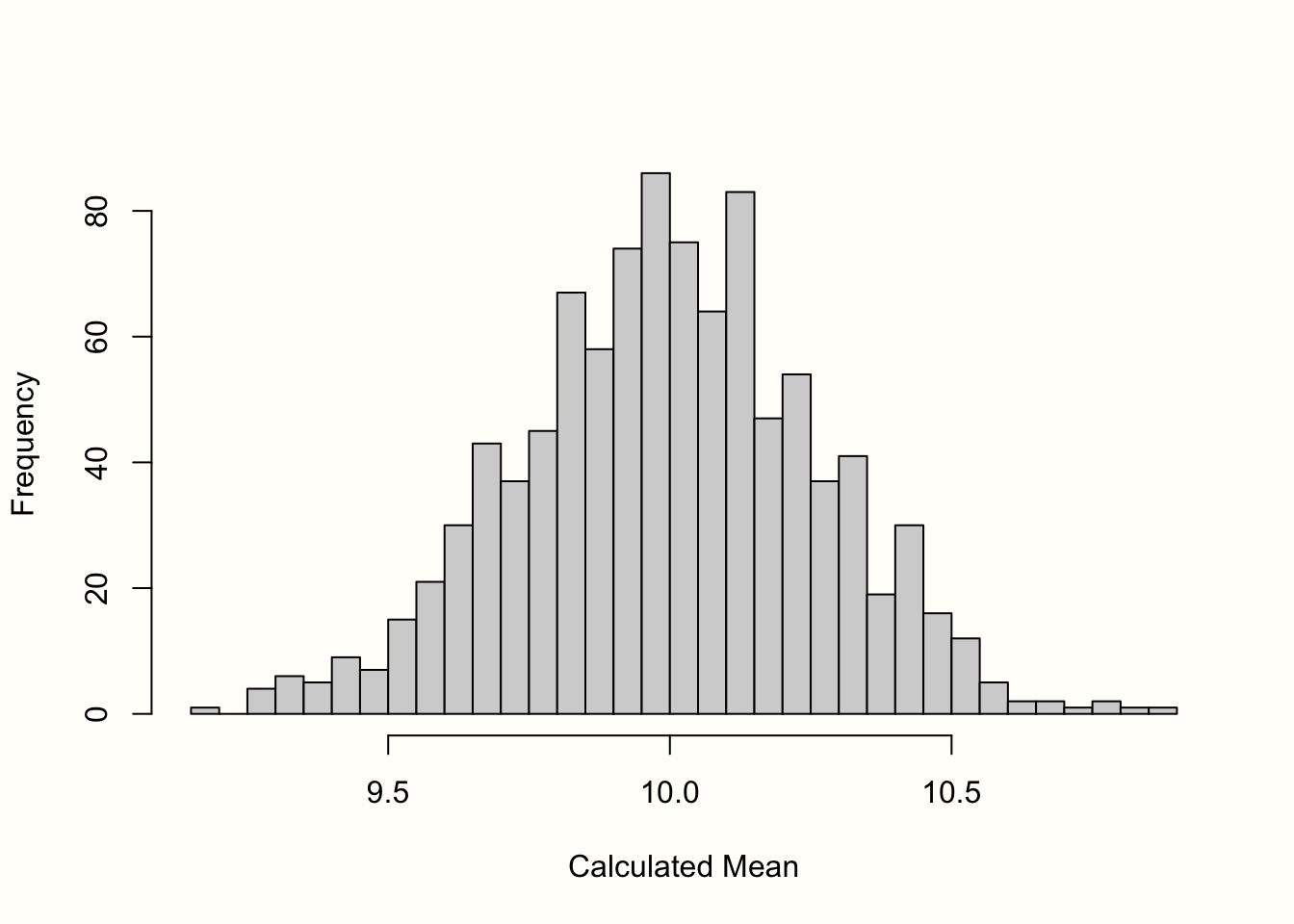
Figure 3.1: 平均値の「サンプル分布」 (1000 件のサンプル)。

標準誤差はこのサンプル分布の標準偏差と定義される。そこで、標準誤差の近似値を得るために、1000 個の模擬平均の標準偏差を計算しておいた。その結果、$SE =$ 0.267 となる。

前にも述べたように、現実世界ではサンプル分布をシミュレーションして標準誤差を計算することはできない。しかし、統計理論に基づいた公式があるので、観測されたサンプルが1つしかない (通常の) 場合でも、標準誤差の推定値を計算することが可能である)。平均値の標準誤差を計算する公式は次のように定義されている。

\[\begin{align} SE = \frac{s}{\sqrt{n}} \tag{3.2} \end{align}\]

つまり、サンプル $s$ の標準偏差をサンプルサイズ $n$ の平方根で割ったものを標準誤差と定義している。この式を使って、 R を使う前に作った sample オブジェクトの標準誤差を簡単に計算することが可能である。ランダムサンプルのサイズは $n =$ 50 であったことを思い出す。

sd(sample)/sqrt(50)

## [1] 0.2618756

この値をサンプル分布のシミュレーションで求めた値と比較すると、ほぼ同じであることがわかる。この公式を使えば、手持ちのサンプルだけで、かなり正確に標準誤差を推定することができるのである。

式 3.2 から、平均値の標準誤差は研究のサンプルサイズに依存することがわかる。$n$ が大きくなると標準誤差は小さくなり、真の母平均の推定値がより正確になることを意味している。

この関係を説明するために、別のシミュレーションを行おう。ここでも、rnorm 関数を使用し、母集団の平均を $\mu =$ 10、$\sigma =$ 2 とする。しかし、今回は、$n =$ 2 から $n =$ 500 まで、サンプルサイズを変化させる。各シミュレーションについて、式 3.2 を用いて、平均と標準誤差を計算する。

## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this
## warning was generated.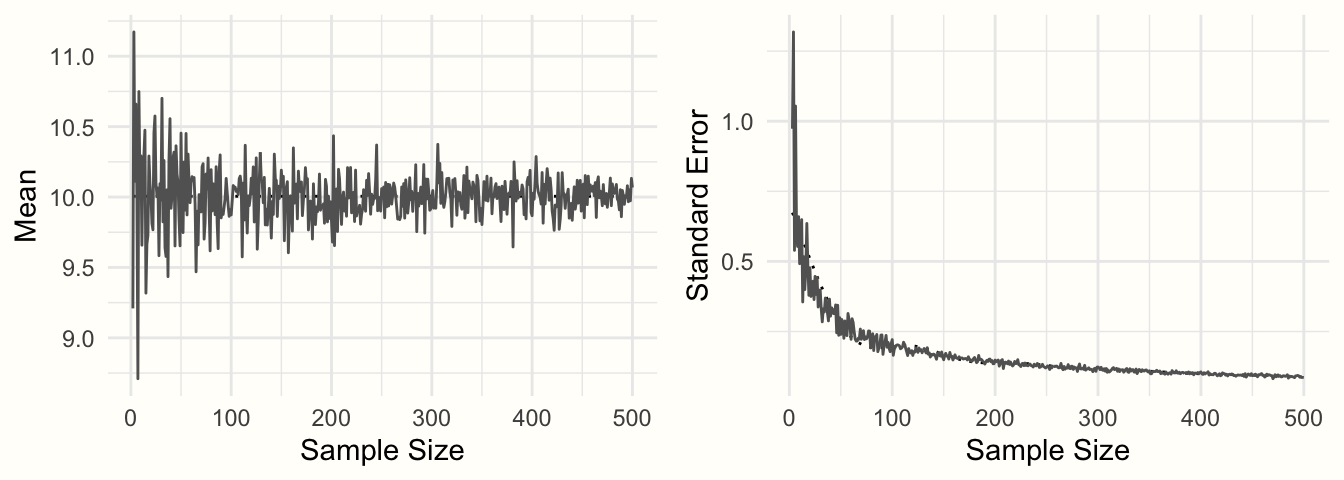

Figure 3.2: サンプルサイズの関数としてのサンプル平均とサンプル誤差。

その結果を Figure 3.2 に示す。サンプルサイズが大きくなるにつれて、平均値の推定値はどんどん正確になっていき、10 に向かって収束していく。この精度の向上は標準誤差で表される。サンプルサイズが大きくなると、標準誤差はどんどん小さくなっていく。

ここまで、メタ分析を行うために必要な要素、すなわち、(１) 観察された効果量またはアウトカム指標、および (２) 標準誤差として表されるその精度について探ってきた。発表された研究からこの2つの情報を算出することができれば、通常はメタ分析合成を行うことも可能である (Chapter 4 参照)。

このシミュレーションでは、例として変数の平均を使用した。上で見た特性は、よく使われる効果量など、他のアウトカム指標でも見られることを理解することが重要である。もし、平均ではなく、サンプルの平均差を計算したとすると、この平均差は、同じような形のサンプル分布を示し、平均差の標準誤差もサンプルサイズが大きくなると小さくなる (標準偏差が同じであることが条件)。例えば、(Fisher’s $z$ 変換された) 相関関係についても同様である。

以下の節では、メタ分析で最も一般的に使用される効果量とアウトカム指標について説明する。これらの効果量測定がよく使われる理由の1つは、本章の最初に定義した2つの基準、すなわち、信頼できる、計算できるを満たしているからである。

式 3.2 で平均値の標準誤差を計算する方法を説明したが、この式は平均値にのみ容易に適用することができる。他の効果量やアウトカム指標では、標準誤差を計算するための公式が異なる。ここで取り上げる効果量の測定基準については、幸いにも公式が存在するので、それらをすべて紹介していこう。公式のコレクションは、Appendixでも見ることが可能である。公式の中にはやや複雑なものもあるが、標準誤差を手動で計算する必要はほとんどない。 R は、この大変な計算を代行してくれる様々な関数がある。

以下の節では、様々な効果量の測定基準についての理論的な議論を提供するだけではない。後で使用する R メタ分析関数が効果量を簡単に計算できるように、データセットにどのような情報を用意しなければならないかも紹介する。

研究デザインの種類ごとに、通常現れる効果量をグループ分けしよう。すなわち、単群デザイン (例: 自然主義研究、調査、非対照試験)、対照群デザイン (例: 実験研究、対照臨床試験) である。これはあくまで大まかな分類であり、厳密なルールではないことに注意したい。ここで提示する効果量の多くは、アウトカムデータの種類が適切であれば、技術的にはどのようなタイプの研究デザインにも適用可能である。

3.2 単群デザインにおける測定値と効果量

3.2.1 平均値

算術平均は、おそらく最もよく使われる中心傾向の尺度である。平均がアウトカム指標として使われることはあまりないが、メタ分析では簡単にプールすることが可能である。例えば、男性の平均身長をセンチメートルやインチで表現し、いくつかの代表的な研究をプールして調査することが可能である。

算術平均は、サンプル中の個々の値 $x_i$ をすべて合計し、その合計をサンプルサイズで割ったものである。

\[\begin{equation} \bar{x} = \frac{\sum^{n}_{i=1}x_i}{n} \tag{3.3} \end{equation}\]

平均の標準誤差の求め方は、すでに説明した (Chapter 3.1 参照)。サンプルの標準偏差 $s$ をサンプルサイズの平方根で割ればいいだけである。

\[\begin{equation} SE_{\bar{x}} = \frac{s}{\sqrt{n}} \tag{3.4} \end{equation}\]

先に見たように、 R では平均とその標準誤差を簡単に計算することが可能である。

# 再現性のために123のシードを設定する
# そして、無作為にサンプルを取る (n=50)
set.seed(123)
sample <- rnorm(n = 50, mean = 20, sd = 5)

# 平均値を計算する
mean(sample)

## [1] 20.17202

# 標準誤差を計算する
sd(sample)/sqrt(50)

## [1] 0.6546889

平均値のメタ分析を行うには、データセットに少なくとも以下の列が含まれている必要がある。

n. 研究の観測数 (サンプルサイズ)。
mean. 研究で報告された平均値。
sd. 研究で報告された変数の標準偏差。

3.2.2 割合

割合 (proportion) もまた、中心傾向の測定方法である。割合は、サンプルのうち何件が特定のサブグループに分類されるかを指定する。割合は、0 から 1 の値を取ることができ、100 を掛けることでパーセントに変換することができる。割合は、例えば、ある時点の病気の有病率を調べたいときに、アウトカム指標として使われることがある。割合 $p$ を計算するためには、特定のサブグループに属する個人の数 $k$ を全サンプルサイズ $n$ で割る必要がある。

\[\begin{equation} p = \frac{k}{n} \tag{3.5} \end{equation}\]

割合の標準誤差は、以下のように計算することができる。

\[\begin{equation} SE_{p} = \sqrt{\frac{p(1-p)}{n}} \tag{3.6} \end{equation}\]

以下のコードを使って、 R の割合とその標準誤差を計算することが可能である。

# k と n に以下の値を定義する。
k <- 25
n <- 125

# 割合を計算する
p <- k/n
p

## [1] 0.2

# 標準誤差を計算する
sqrt((p*(1-p))/n)

## [1] 0.03577709

割合の範囲が 0 と 1 の間に制限されていることが問題になることがある (Lipsey and Wilson 2001, chap. 3)。$p$ が 0 または 1 に近いと、標準誤差が人為的に圧縮され、割合の推定値の精度が過大評価されることになる。

これは、サンプル分布と関係がある。$p$ の値が非常に小さいか大きい場合、サンプル分布は Figure 3.1 のような正規分布になることはほとんどない。0-1 の範囲外の計算された割合を持つランダムなサンプルは不可能であるため、分布は右側に裾が伸びる (right-skewed) か、または左側に裾が伸びる (left-skewed)。

これを避けるために、割合をプールする前に logit 変換するのが一般的である。logit 変換では、まずオッズを計算する (Chapter 3.3.2.2 参照)。オッズは、特定のカテゴリーに該当する参加者の割合を、そのカテゴリーに該当しない参加者の割合で割ったものとして定義される。

そして、自然対数関数 $\log_e$ を使って、オッズを $p=$ 0.5 が値 0 に等しく、かつ範囲制限のない形式に変換している。これにより、サンプル分布がほぼ正規分布となり、標準誤差にバイアスがないことが確認できる。

logit 変換された割合とその標準誤差は以下の式で計算できる (Lipsey and Wilson 2001, chap. 3)¹⁰:

\[\begin{equation} p_{\text{logit}} = \log_{e} \left(\frac{p}{1-p}\right) \tag{3.7} \end{equation}\]

\[\begin{equation} SE_{p_{\text{logit}}} = \sqrt{\frac{1}{np}+\frac{1}{n(1-p)}} \tag{3.8} \end{equation}\]

幸い、 R のメタ分析機能を使えば、この logit 変換を自動的に行ってくれる。そのため、データセットには以下の列を用意するだけでよい。

event. 特定のサブグループ ($k$) に含まれる観測数。
n. サンプルサイズの合計 $n$。

3.2.3 相関関係

3.2.3.1 ピアソン積率相関

相関とは、2つの変数間の共分散の大きさを表す効果量である。最も一般的なのは、2つの連続変数に対して計算できるピアソン積率相関 (Pearson Product-Moment Correlation)¹¹であり、この積率相関は、例えば、メタ分析の研究者が2つの変数の間の共分散の量を表す効果量として用いることが可能である。積率相関は、例えば、メタ分析で関係の質と幸福度の関係を調べたいときに、効果量として使うことができる。

変数 $x$ と変数 $y$ の相関 $r_{xy}$ は、$x$ と $y$ の 共分散 $\text{Cov}(x,y)=\sigma^{2}_{xy}$ を、それらの標準偏差$\sigma_x$ と $\sigma_y$ の積で割ったもので定義される。

\[\begin{equation} r_{xy} = \frac{\sigma^{2}_{xy}}{\sigma_x \sigma_y} \tag{3.9} \end{equation}\]

サンプルサイズ $n$ を用いると、$r_{xy}$ の標準誤差は次のように計算できる。

\[\begin{equation} SE_{r_{xy}} = \frac{1-r_{xy}^2}{\sqrt{n-2}} \tag{3.10} \end{equation}\]

積率相関を計算するとき、2つの変数の間の共変動をそれらの標準偏差で標準化する。つまり、2つ以上の研究が同じ尺度で構成要素を測定していれば、あまり意味がなく、相関を計算すれば、自動的に効果を比較することが可能になる。

相関は -1 ～ 1 の値をとる。相関の大きさは、しばしば Cohen (1988) の慣例を用いて解釈される。

$r \approx$ 0.10: 小さい効果。
$r \approx$ 0.30: 中程度の効果。
$r \approx$ 0.50: 大きい効果。

しかし、これらの慣例はあくまで経験則であることに留意すべきである。対象や先行研究に応じて、相関の大小を定量化する方がはるかに良い場合が多いのである。

残念ながら、相関は割合 (Chapter 3.2.2) と同様に範囲が限定されており、サンプルサイズの小さい研究に対して標準誤差を推定する際にバイアスをもたらす可能性がある (Alexander, Scozzaro, and Borodkin 1989)。

そのため、メタ分析では相関を Fisher’s $z$¹² に変換することが一般的である。これも logit 変換と同様に、サンプル分布がほぼ正規分布になるように自然対数関数を用いる (詳しい説明は、Chapter 3.3.2 を参照)。式は次のようになる。

\[\begin{equation} z = 0.5\log_{e}\left(\frac{1+r}{1-r}\right) \tag{3.11} \end{equation}\]

サンプルサイズ $n$ がわかれば、Fisher’s $z$ の近似標準誤差はこの式で求めることができる (Olkin and Finn 1995)。

\[\begin{equation} SE_{z} = \frac{1}{\sqrt{n-3}} \tag{3.12} \end{equation}\]

また、 R では cor と log 関数を用いて $r_{xy}$ と $z$ を直接計算することが可能である。

# 2 つの連続変数 x と y をシミュレート
set.seed(12345)
x <- rnorm(20, 50, 10)
y <- rnorm(20, 10, 3)

# x と y の相関を計算する
r <- cor(x,y)
r

## [1] 0.2840509

# Fisher's z を計算する
z <- 0.5*log((1+r)/(1-r))
z

## [1] 0.2920831

ありがたいことに、 R の相関のメタ分析を行う際に、Fisher’s $z$ 変換を手動で行う必要はない。データセットに必要な列は以下の通りである。

cor. ある研究の (変換されていない) 相関係数。
n. 研究のサンプルサイズ。

3.2.3.2 点双列相関

ピアソン積率相関は、2つの連続変数間の関係を記述する。一方の変数 $y$ だけが連続的で、もう一方の変数 $x$ が二値的 (つまり、2つの値だけをとる) な場合、$x$ の因子の割合と因子ごとの $y$ 平均値から、$y$ がどれだけ予測できるかを表す点双列相関 (point-biserial correlation) を計算することができる。

点双列相関は、以下の式で計算できる。

\[\begin{equation} {r_{pb}}= \frac{(\bar{y_1}-\bar{y_2})\sqrt{p_1(1-p_1)}}{s_y} \tag{3.13} \end{equation}\]

この式で、$\bar{y_1}$ は二項変数 $x$ の第1群のみを考えたときの連続変数の平均、$\bar{y_2}$ は $x$ の第2群のみを考えたときの平均、$p_1$ は $x$ の第1群に該当する症例の割合、$s_y$ は $y$ の標準偏差とする。

点双列相関は、 R で cor 関数を使って計算することができる (前節を参照)。与えられた変数の1つが2つの値しかとらず、もう1つが連続的である場合、(近似的な) 点双列相関が自動的に計算される。

点双列相関は、後述する標準化平均差とよく似ている (Chapter 3.3.1.2)。どちらの効果量指標も、連続変数の値が 2 群間でどれだけ異なるかを定量化するものである。しかし、点双列相関がメタ分析でプールされることはあまり一般的ではない。積率相関と同様に、点双列相関は、群比率が同じでない場合に範囲制限を受けるなど、メタ分析には好ましくない統計的性質を持っている (Bonett 2020)。

連続的なアウトカム変数の群間差に興味がある場合、メタ分析のために点双列相関を標準化平均差に変換することが推奨される (Lipsey and Wilson 2001, chap. 3)。点双列相関を標準化平均差に変換する公式は、本書の「各種ツール」の Chapter 17.3 に掲載されている。

3.3 対照群デザインにおける効果量

3.3.1 (標準化) 平均差

3.3.1.1 群間平均差

群間平均差 (group between mean difference) $\text{MD}_{\text{between}}$ は、2つの 独立した 群間の平均の未標準化の差として定義される。群間平均差は、対照試験や他のタイプの実験的研究で通常見られるように、研究が少なくとも2つの群を含んでいる場合に計算することが可能である。メタ分析では、すべての研究が全く同じ尺度でアウトカムを測定した場合のみ、平均値を使用することが可能である。例えば、体重は科学研究においてほぼ常にキログラムで測定され、糖尿病学では、HbA$_{\text{1c}}$値が血糖値の測定に一般的に使用される。

平均差は、グループ1の平均値 $\bar{x}_1$ からグループ2の平均値 $\bar{x}_2$ を引いた値と定義される。

\[\begin{equation} \text{MD}_{\text{between}} = \bar{x}_1 - \bar{x}_2 \tag{3.14} \end{equation}\]

標準誤差は、この式で求めることができる。

\[\begin{equation} SE_{\text{MD}_{\text{between}}} = s_{\text{pooled}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}} \tag{3.15} \end{equation}\]

式中、$n_1$ はグループ 1 のサンプルサイズ、$n_2$ はグループ 2 のサンプルサイズ、$s_{\text{pooled}}$ は両群のプール標準偏差 (pooled standard deviation) であることを表している。グループ 1 の標準偏差 ($s_1$) とグループ 2 の標準偏差 ($s_2$) を用いて、$s_{\text{pooled}}$ の値は以下のように計算することができる。

\[\begin{align} s_{\text{pooled}} = \sqrt{\frac{(n_1-1)s^2_1+(n_2-1)s^2_2}{(n_1-1)+(n_2-1)}} \tag{3.16} \end{align}\]

ここでは、R で平均差とその標準誤差を計算する例を示す。まず初めに、データをシミュレートしよう。これは、実行可能な値を得るためにのみ行う。実際のメタ分析においては、x1 と x2 の平均値およびその標準偏差 s1 と s2 は、出版された論文から抽出できるであろうし、各群のサンプルサイズ n1 と n2 も同様である。このため、ここで示すものはそれほど重要ではない。

# 母平均が異なる2つの確率変数を生成する
set.seed(123)
x1 <- rnorm(n = 20, mean = 10, sd = 3)
x2 <- rnorm(n = 20, mean = 15, sd = 3)

# 数式に必要な値を計算する
s1 <- sd(x1)
s2 <- sd(x2)
n1 <- 20
n2 <- 20

このデータを使って、平均差とその標準誤差を、以前の式を使って計算していきたい。

# 差の平均を計算する
MD <- mean(x1) - mean(x2)
MD

## [1] -4.421357

# s_pooled を計算する
s_pooled <- sqrt(
  (((n1-1)*s1^2) + ((n2-1)*s2^2))/
    ((n1-1)+(n2-1))
)

# 標準誤差を計算する
se <- s_pooled*sqrt((1/n1)+(1/n2))
se

## [1] 0.8577262

通常、これらの計算をここで示したように手作業で行う必要はない。平均値の差のメタ分析では、データセットに以下の列を用意するだけでよい。

n.e. 介入・実験群の観測数。
mean.e. 介入・実験群の平均値。
sd.e. 介入・実験群の標準偏差。
n.c. 対照群の観測数。
mean.c. 対照群の平均値。
sd.c. 対照群の標準偏差。

3.3.1.2 群間標準化平均差

群間の標準化平均差 (standardized mean difference, SMD) $\text{SMD}_{\text{between}}$ は、プールした標準偏差 $s_{\text{pooled}}$ で標準化した、独立した2群間の平均値の差と定義される。文献では、標準化平均差は、心理学者で統計学者の Jacob Cohen にちなんで命名された Cohen’s $d$ とも呼ばれる。

標準化されていない平均差とは対照的に、$\text{SMD}_{\text{between}}$ は2群間の差を標準偏差の単位で表現する。これは、2つのグループの生の平均差 $\bar{x_1}$ と $\bar{x_2}$ を、両グループのプール標準偏差 $s_{\text{pooled}}$ で割ることにより実現できる。

\[\begin{equation} \text{SMD}_{\text{between}} = \frac{\bar{x}_1 - \bar{x}_2}{s_{\text{pooled}}} \tag{3.17} \end{equation}\]

ここで、$s_{\text{pooled}}$ は、既に取り上げた式 (3.16) を用いて計算する。メタ分析では標準化平均差の方が非標準化平均差よりもずっとよく使われる。これは、$\text{SMD}_{\text{between}}$ が研究間で比較できるためで、それぞれの研究が同じ測定器を使ってアウトカムを測定していなかったとしても、比較することが可能になる。

標準化によって、$\text{SMD}_{\text{between}}=$ 1 は常に2群の平均が互いに 1 サンプル標準偏差離れていることを意味し (Figure 3.3 参照)、$\text{SMD}_{\text{between}}=$ 2 は2標準偏差の差を表す、という効果がある¹³。

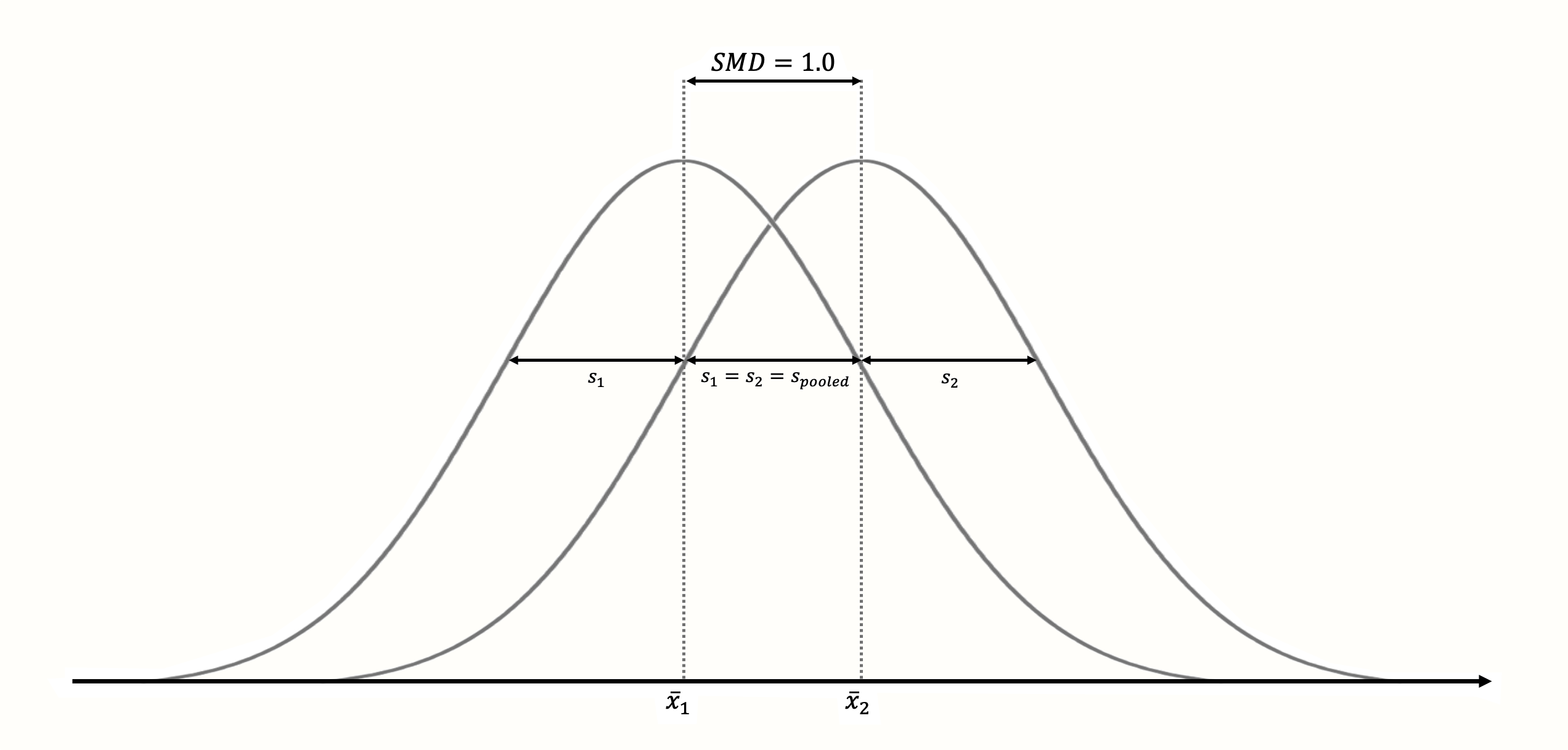
Figure 3.3: 標準化平均差が1 (正規性、標準偏差が等しく、両群のサンプルサイズが等しいと仮定した場合)。

標準化することで、平均値の差の大きさを評価することが非常に容易になる。標準化された平均値の差は、Cohen (1988) による慣例を用いて解釈されることが多い。

SMD $\approx$ 0.20: 小さい効果。
SMD $\approx$ 0.50: 中程度の効果。
SMD $\approx$ 0.80: 大きい効果。

ピアソン積率相関と同様 (Chapter 3.2.3.1)、経験則に過ぎない。

通常、標準化された平均値の差は、その「現実的な」意味合いに基づいて解釈する方がずっと良いのである。効果量は Cohen の基準では小さいかもしれないが、それでも非常に重要である可能性がある。例えば、多くの深刻な病気では、統計的な効果が非常に小さくても、集団レベルでは大きな影響を与え、何百万人もの命を救う可能性があるのである。ある研究では、うつ病の治療において、$\text{SMD}_{\text{between}}=$ 0.24 のような小さな効果でさえ、患者の命に臨床的に重要な影響を与えることができることが示された (Pim Cuijpers et al. 2014)。

この式を使って$\text{SMD}_{\text{between}}$ の標準誤差を計算することができる (Borenstein et al. 2011)。

\[\begin{equation} SE_{\text{SMD}_{\text{between}}} = \sqrt{\frac{n_1+n_2}{n_1n_2} + \frac{\text{SMD}^2_{\text{between}}}{2(n_1+n_2)}} \tag{3.18} \end{equation}\]

ここで、$n_1$ と $n_2$ はグループ 1 とグループ 2 のサンプルサイズであり、$\text{SMD}_{\text{between}}$ は計算された群間標準化平均差である。

R には、$\text{SMD}_{\text{between}}$ /Cohen’s $d$ を一度に計算できる関数がいくつかある。ここでは、{esc} パッケージ (Lüdecke 2019) に含まれる esc_mean_sd 関数を使用する。このパッケージは今まで使用したことがないので、まずインストールする必要がある (Chapter 2.2 参照)。

# esc パッケージのロード
library(esc)

# SMD/d を計算するために必要なデータを定義する。
# 医かは、例として作ったダミーデータ
grp1m <- 50   # group 1 の平均値
grp2m <- 60   # group 2 の平均値
grp1sd <- 10  # group 1 の標準偏差
grp2sd <- 10  # group 2 の標準偏差
grp1n <- 100  # group1 のサンプルサイズ
grp2n <- 100  # group2 のサンプルサイズ

# 効果量を計算する
esc_mean_sd(grp1m = grp1m, grp2m = grp2m, 
            grp1sd = grp1sd, grp2sd = grp2sd, 
            grp1n = grp1n, grp2n = grp2n)

## Effect Size Calculation for Meta Analysis
## 
##      Conversion: mean and sd to effect size d
##     Effect Size:  -1.0000
##  Standard Error:   0.1500
##            [...]

この出力では、言及すべきことが2つある。まず、計算された標準化平均の差がちょうど 1 であることがわかる。これは、私たちが定義した 2 つの平均の差が (プールされた) 標準偏差と等しいので、理にかなっている。

次に、効果量がマイナスであることがわかる。これは、グループ 2 の平均がグループ 1 の平均より大きいからである。これは数学的には正しいのであるが、他の人がより簡単に解釈できるように、計算された効果量の符号を変えなければならないことがある。

この例のデータは、介入 (group 1) または介入なし (group 2) を受けた後、人々が1週間に吸うタバコの平均本数を測定した研究から得られたと想像する。この文脈では、介入群では平均喫煙本数が少なかったので、研究結果は肯定的であったとする。したがって、効果量を -1.0 ではなく 1.0 と報告することは理にかなっており、他の人が直感的に介入には正の効果があったと理解できるようになる。

効果量の符号が特に重要になるのは、ある研究では高い値が良いアウトカムを意味し、他の研究では低い値が良いアウトカムを意味する尺度を用いた場合である。この場合、すべての効果量が一貫して同じ方向にコード化されていることが不可欠である (例えば、メタ分析のすべての研究で、効果量が大きいほど介入群における転帰が良いことを意味することを確認する必要がある)。

多くの場合、標準化平均差に対して小サンプル補正を行い、Hedges’ $g$ と呼ばれる効果量になる。この補正については、Chapter 3.4.1 で取り上げる。

標準化平均差のメタ分析を行うには、データセットに少なくとも以下の列が含まれている必要がある。

n.e. 介入・実験群の観測数。
mean.e. 介入・実験群の平均値。
sd.e. 介入・実験群の標準偏差。
n.c. 対照群の観測数。
mean.c. 対照群の平均値。
sd.c. 対照群の標準偏差。

標準偏差の外部推定値による標準化

SMD を計算するとき、$s_{\text{pooled}}$ を使うのは、それが母集団における真の標準偏差の代理として機能するからである。しかし、特に研究の規模が小さい場合、サンプルに基づいて計算された標準偏差は、母集団の標準偏差の推定値としては不適切な場合がある。

この場合、可能な解決策は、平均差を標準化するために $s_{\text{pooled}}$ の外部推定値を使用することである (Julian Higgins et al. 2019)。このような外部推定値は、類似の集団でこの研究と同じ測定器を使用した大規模な横断研究から抽出されるかもしれない。

3.3.1.3 群内 (標準化) 平均差

群内の差を調べる場合、非標準化または標準化された平均差を計算することが可能である。これは通常、同じグループの人々が2つの異なる時点 (例えば、介入前と介入後) で測定される場合である。

群間平均差とは異なり、$\text{(S)MD}_{\text{within}}$は独立ではないデータを用いて計算される。例えば、測定点 $t_1$ での人物 $i$ の値が、測定点 $t_2$ での同じ人物の値に影響を与えている可能性がある。群内平均差は、通常、異なる時点で測定されたデータに基づいていることから、** (標準化) 平均利得** ((standardized) mean gain)とも呼ばれる。

群内平均差 $\text{MD}_{\text{within}}$ は、同じ群の $t_1$ と $t_2$ の2つの時点の値を比較するようになった以外は、$\text{MD}_{\text{between}}$ と同じ方法 ( Chapter 3.3.1.1 参照) で計算される。

\[\begin{equation} \text{MD}_{\text{within}} = \bar{x}_{\text{t}_2} - \bar{x}_{\text{t}_1} \tag{3.19} \end{equation}\]

群内平均差の標準化版を計算したい場合は、より複雑になる。$\text{SMD}_{\text{within}}$ をどのように計算すべきかについて、完全なコンセンサスはない。ブログ記事で、Jake Westfall は少なくとも5つの異なる計算方法があることを指摘している。

直感的なオプションは、両評価点のプールされた標準偏差 $s_{\text{t}_1}$ と $s_{\text{t}_2}$ を使って平均 $\text{MD}_{\text{within}}$ を標準化することである。群内デザインでは観測点数が通常同じなので、2つの標準偏差の二乗の和を2で割って $s^2_{\text{pooled}}$ を求めればよいことになる。そうでない場合は、Chapter 3.3.1.1 の式 (3.16) を使って $s_{\text{pooled}}$ を計算することが可能である。このことから、以下の式が導かれる。

\[\begin{equation} \text{SMD}_{\text{within}} = \frac{\bar{x}_{\text{t}_2} - \bar{x}_{\text{t}_1}}{s_{\text{pooled}}} \tag{3.20} \end{equation}\]

Becker (1988) は、さらに良い解決策を提案した。すなわち、$\text{MD}_{\text{within}}$ を介入前の得点の標準偏差 ($s_{\text{t}_1}$) で割ることである。この理由は、$s_{\text{t}_1}$ の方が介入効果の影響を受けにくいことがある¹⁴。

\[\begin{equation} \text{SMD}_{\text{within}} = \frac{\bar{x}_{\text{t}_2} - \bar{x}_{\text{t}_1}}{s_{\text{t}_1}} \tag{3.21} \end{equation}\]

また、$\text{MD}_{\text{within}}$ と $\text{SMD}_{\text{within}}$ の標準誤差はこれらの式を使って計算可能である (Borenstein et al. 2011, chap. 4; Becker 1988)。

\[\begin{equation} SE_{\text{MD}_{\text{within}}}=\sqrt{\dfrac{s^2_{\text{t}_1}+s^2_{\text{t}_2}-(2r_{\text{t}_1\text{t}_2}s_{\text{t}_1}s_{\text{t}_2})}{n}} \tag{3.22} \end{equation}\]

\[\begin{equation} SE_{\text{SMD}_{\text{within}}} = \sqrt{\frac{2(1-r_{\text{t}_1\text{t}_2})}{n}+\frac{\text{SMD}^2_{\text{within}}}{2n}} \tag{3.23} \end{equation}\]

群内 (標準化) 平均値の差の標準誤差を計算するために、評価点間の相関 $r_{\text{t}_1\text{t}_2}$ が必要であることは、実際には問題となることが多い。変数の前後相関は発表された研究でほとんど報告されていないため、先行研究に基づいて $r_{\text{t}_1\text{t}_2}$ の値を仮定せざるを得ない。

しかし、相関を正確に把握しないと、結果に誤差が生じる可能性がある。一般的に、メタ分析で群内効果量を計算することは避けた方が良いと言われている (Pim Cuijpers et al. 2017)。特に、実験群と対照群の両方のデータがある場合は、前後比較ではなく、$t_2$ における群間 (標準化) 平均差を計算して、治療の効果を測定する方がずっと良い。ただし、対照群を含まない研究のみにメタ分析を行う場合は、群内平均差を計算することが可能である。

群内標準化平均差 (群内 (within-group) Cohen’s $d$ とも呼ばれる) は R でこのように計算できる。

# 効果量計算に必要なデータ例を定義
x1 <- 20    # t1 における平均値
x2 <- 30    # t2 における平均値
sd1 <- 13   # t1 における標準偏差
n <- 80     # サンプルサイズ
r <- 0.5    # t1 と t2 の相関係数

# 生の平均差を計算
md_within <- x2 - x1

# smd を計算:
# ここで、t1 における標準偏差
# を使い、平均差を標準化する
smd_within <- md_within/sd1
smd_within

## [1] 0.7692308

# 標準誤差を計算
se_within <- sqrt(((2*(1-r))/n) + 
              (smd_within^2/(2*n)))
se_within

## [1] 0.1272722

群内 (標準化) 平均差のメタ分析は、 R では事前に計算された効果量を用いてのみ実行可能となる (Chapter 3.5.1 参照)。今回のデータセットでは、以下の列が必要である。

TE: 算出された群内効果量。
seTE: 群内効果量の標準誤差。

標準化の限界

標準化平均差は、間違いなくメタアナリシスで最も頻繁に使用される効果量の指標の1つである。Chapter 3.3.1.2 で述べたように、標準化により、少なくとも理論的には、異なる研究で観察された効果の強さを比較することができる。

しかし、標準化は、「免罪符」ではない。ある研究の $\text{SMD}$ の大きさは、そのサンプルの多様性に大きく依存する (Viechtbauer 2007a も参照)。2 つの同じ研究を行い、アウトカムを測定するために同じ測定器を使用するが、この 2 つの研究は大幅に異なる分散を持つ 2 つの集団で行われたと想像してみよう。この場合、両研究の「生の」平均差が同じであっても、両研究の $\text{SMD}$ 値は大きく異なるであろう。

この場合、一方の研究の効果の「因果」の強さが他方よりはるかに大きいか小さいかを論じることはやや困難である。Jacob Cohen (1994) が有名な論文でと述べたように、「私にとっての A の B に対する効果は、私が大きく変動するグループにいるか[…]、まったく変動しない別のグループにいるかには、ほとんど依存しない」(p. 1001)。ところで、この問題は、一般に使用されている「標準化された」メタアナリシスにおける効果量の測定、例えば相関関係にも当てはまる。

さらに、標準化する単位は、思ったよりも明確に定義されていないことが多いことも見た。群間と群内の $\text{SMD}$s には様々な選択肢があり、特定の研究でどのアプローチが選ばれたかを切り分けるのは難しい。メタ分析のための標準化効果量の計算方法については、常に研究間で可能な限り一貫性を保つことが必要である。それでも、たとえ標準化を行ったとしても、効果量の一致度には限界があることを心に留めておく必要がある。

もちろん、アウトカムがすべての研究で結果が同じ尺度で測定され、生平均差が利用できれば、最高の解決策になるであろう。しかし、多くの研究分野では、そのような方法論的な調和からはほど遠いところにいるのが現状である。したがって、残念ながら、標準化効果量は、第二の最良の選択肢となることもある。

3.3.2 リスク比とオッズ比

3.3.2.1 リスク比

リスク比 (別名: 相対リスク) とは、その名の通り、2つのリスクの比のことである。リスクとは基本的に割合 (proportion) のことである (Chapter 3.2.2 参照)。リスクは、バイナリ (二値) データを扱う場合に計算可能である。

このようなアウトカムは、医学研究において、病気の発症や死亡のリスクを調べる場合によく見られるため、「割合」ではなく「リスク」という用語を使用する。このような事象は、イベントと呼ばれる。治療群と対照群からなる対照臨床試験を行っているとする。ここで興味があるのは、研究期間中に何人の患者があるイベント $E$ を経験したかである。

このような研究から得られる結果は、$2 \times 2$ の表に分類できる (Schwarzer, Carpenter, and Rücker 2015, chap. 3.1)。

Table 3.1: 二値アウトカムを用いた対照研究の結果。
	Event	No Event
Treatment	$a$	$b$	$n_{\text{treat}}$
Control	$c$	$d$	$n_{\text{control}}$
	$n_E$	$n_{\neg E}$

このデータに基づいて、治療群と対照群の両方について、調査期間中にイベント $E$ を経験するリスクを計算することが可能である。$E$ を経験した人の数を、その群の総サンプルサイズで割ればよいのである。

したがって、治療群のリスクである ${p_{E}}_{\text{treat}}$ は、次のように計算される。

\[\begin{equation} {p_{E}}_{\text{treat}} = \frac{a}{a+b} = \frac{a}{n_{\text{treat}}} \tag{3.24} \end{equation}\]

そして、対照群のリスク、${p_{E}}_{\text{control}}$ は、以下のようになる。

\[\begin{equation} {p_{E}}_{\text{control}} = \frac{c}{c+d} = \frac{c}{n_{\text{control}}} \tag{3.25} \end{equation}\]

そして、リスク比は、治療・介入群のリスクを対照群のリスクで割ったものと定義される。

\[\begin{equation} \text{RR} = \frac{{p_{E}}_{\text{treat}}}{{p_{E}}_{\text{control}}} \tag{3.26} \end{equation}\]

${p_{E}}_{\text{treat}}$ と ${p_{E}}_{\text{control}}$ はどちらも 0 と 1 の間の値しか持ち得ないので、RR はいくつかの興味深い性質を持っている。まず、リスク比が負になることはない。次に、治療群と対照群の間に差がない場合、RR は (SMD のように 0 ではなく) 1 という値になる。RR が 1 より大きければ、治療群がイベント $E$ のリスクを増加させることを意味し、RR が 1 より小さければ、介入によってリスクが減少することを意味する。

RR の特徴は、同じ大きさの効果は等価ではないということである。例えば、RR $=$ 0.5 は、介入群でリスクが半分になることを意味する。これはリスク比が正規分布に従わないことを意味し、メタ分析では問題になることがある。

この問題を避けるために、統合する前にリスク比を 対数リスク比 (log-risk ratio) に変換することもよくある。これにより、漸近正規性、効果量が任意の値になること、値が 0 (効果がないことを意味する) を中心になることが保証される。この変換は、RR の自然対数を取ることによって行われる。

\[\begin{equation} \log \text{RR} = \log_{e}(\text{RR}) \tag{3.27} \end{equation}\]

そして、対数リスク比の標準誤差は、この式を用いて計算することができる。

\[\begin{equation} SE_{\log \text{RR}} = \sqrt{\frac{1}{a}+\frac{1}{c} - \frac{1}{a+b} - \frac{1}{c+d}} \tag{3.28} \end{equation}\]

R の (対数) リスク比はこのように計算することができる。

# データを定義
a <- 46         # 治療群のイベント数
c <- 77         # 対照群のイベント数
n_treat <- 248  # 治療群のサンプルサイズ
n_contr <- 251  # 対照群のサンプルサイズ

# リスクを計算
p_treat <- a/n_treat
p_contr <- c/n_contr

# リスク比を計算
rr <- p_treat/p_contr
rr

## [1] 0.6046292

# 対数リスク比と標準誤差を計算
log_rr <- log(rr)
log_rr

## [1] -0.5031398

se_log_rr <- sqrt((1/a) + (1/c) - (1/n_treat) - (1/n_contr))
se_log_rr

## [1] 0.1634314

ゼロセルがあると、リスク比の計算が難しくなる。実際には、$a$ または $c$ (あるいはその両方) がゼロであることがあり、これは治療群でも対照群でもイベントが記録されていないことを意味する。RRの計算式を見ると、なぜこれが問題なのかがよくわかる。$a$ (治療群のイベント) がゼロなら、${p_{E}}_{\text{treat}}$ もゼロで、RR はゼロになる。$c$ がゼロの場合はさらに問題で、${p_{E}}_{\text{control}}$ がゼロということになり、ゼロで割れない ということがわかる。

この問題は、連続性補正 (continuity correction) を用いて対処されることがよくある。最も一般的な連続性補正の方法は、ゼロになっている全てのセルに0.5の増分を加えることである (Gart and Zweifel 1967) 。また、対照群と治療群のサンプルサイズが非常に不均等な場合は、治療群連続性補正 (Sweeting, Sutton, and Lambert 2004) を用いることもできる。

しかし、そのような補正は偏った結果につながるという証拠もある (Efthimiou 2018)。(固定効果) Mantel-Haenszel 法というメタ解析のプール手法は、メタ解析のすべての研究にゼロセルが存在しない限り、補正せずに扱うことが可能である。したがって、後者のシナリオに当てはまらない限り、連続性補正は避けた方がよいだろう。

ゼロセル問題の特殊な形として、ダブルゼロスタディがある。これは、$a$ と $c$ の両方がゼロである研究である。直感的には、このような研究の結果は、介入群と対照群のリスクが同程度であり、RR=1であることを意味していると考えるだろう。

残念ながら、そう簡単ではない。2つのグループの間に本当の効果があるけれども、その差を検出するにはサンプルサイズが小さすぎたということは大いにあり得る。特に、$E$ が発生する確率が非常に低い場合には、この可能性が高くなる。

あるマッドサイエンティストが、雷に打たれる危険を減らすとされる薬、Fulguridone の効果を評価する無作為化比較試験を行ったとする。彼は100人を薬物投与群と対照群のどちらかに均等に割り振り、3年間観察した。試験の結果は、治療群でも対照群でも雷に打たれた人はいなかったので、残念な結果になった。しかし、私たちは、雷に打たれる可能性がどれほど低いか、一般的に知っている。たった100人の観察では、たとえ治療が効くという奇妙な考えを受け入れたとしても、このような稀な出来事における違いを検出するには十分ではない。このため、ダブルゼロ研究は、効果をプールする際に完全に捨てられることが多いのである。

リスク比は、ある事象が一般的にどの程度よく起こるかという情報を与えてはくれないのである。メタ分析でリスク比が0.5と報告された場合、例えば、ある介入によってリスクが半分に減少したことがわかる。しかし、リスクが40%から20%に減少したかどうか、あるいは0.004%から0.002%に減少したかどうかはわからない。リスク比が実用的であるかどうかは、文脈に依存する。リスク比0.5が0.002%のリスク低下に相当する場合、集団レベルでは大きな影響を与えないかもしれないが、対象となる事象が例えば重症で衰弱する病気であれば、それでも重要である可能性がある。

R でメタ分析を行う場合、通常、研究の対数リスク比を手作業で計算する必要はない。また、データをインポートする際にも、ゼロセルについて心配する必要はない。以下の列はデータセットに含まれている必要がある。

event.e. 治療群・実験群におけるイベント数。
n.e. 治療群・実験群のサンプルサイズ。
event.c. 対照群におけるイベント数。
n.c. 対照群のサンプルサイズ。

3.3.2.2 オッズ比

リスク比 (Chapter 3.3.2.1) と同様に、オッズ比も2群2値のアウトカムデータがある場合に計算することが可能である。前回の割合の章 (Chapter 3.2.2) で、オッズを「あるカテゴリーに該当する個数を、そのカテゴリーに該当しない個数で割ったもの」と定義したが、今回は「あるカテゴリーに該当する個数を、そのカテゴリーに該当しない個数で割ったもの」と定義する。

Table 3.1 の表記を使うと、治療群と対照群のオッズの計算式は次のようになる。

\[\begin{equation} \text{Odds}_{\text{treat}} = \frac{a}{b} \tag{3.29} \end{equation}\]

\[\begin{equation} \text{Odds}_{\text{control}} = \frac{c}{d} \tag{3.30} \end{equation}\]

オッズが実際に何を意味するのかを正しく解釈するのは難しいだろう。オッズは事象と非事象の比率を表すのであって、事象の確率を表すのではない。3人の個人を調査したとする。2人は興味のある事象を経験し、1人は経験しなかったとする。このデータから、その事象の確率 (またはリスク) は $p = 2/3 \approx 66\%$ となる。しかし、事象の発生確率は、Odds = $\frac{2}{1}$ = 2となり、1人の非事象に対して2人の事象があることになる。

そして、オッズ比 (OR) は、治療群でのオッズを対照群でのオッズで割ったものと定義される。

\[\begin{equation} \text{OR} = \frac{a/b}{c/d} \tag{3.31} \end{equation}\]

リスク比と同様に (Chapter 3.3.2.1 参照)、オッズ比もメタ分析には好ましくない統計的性質を持っている。そのため、オッズ比を自然対数を使って対数オッズ比 (log-odds ratio) に変換することも一般的である。

\[\begin{equation} \log \text{OR} = \log_{e}(\text{OR}) \tag{3.32} \end{equation}\]

対数オッズ比の標準誤差は、この式で計算できる (表記は Table 3.1 を使用する)。

\[\begin{equation} SE_{\log \text{OR}} = \sqrt{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}} \tag{3.33} \end{equation}\]

{esc} パッケージの esc_2x2 関数は、 R における (対数) オッズ比を簡単に計算する方法を提供する。

library(esc)

# データを定義
grp1yes <- 45  # 治療群のイベント数
grp1no <- 98   # 治療群の非イベント数
grp2yes <- 67  # 対照群のイベント数
grp2no <- 76   # 対照群の非イベント数

# es.type に "or" と設定し、OR を計算
esc_2x2(grp1yes = grp1yes, grp1no = grp1no,
        grp2yes = grp2yes, grp2no = grp2no,
        es.type = "or")

## 
## Effect Size Calculation for Meta Analysis
## 
##      Conversion: 2x2 table (OR) coefficient to effect size odds ratio
##     Effect Size:   0.5209
##  Standard Error:   0.2460
##        Variance:   0.0605
##        Lower CI:   0.3216
##        Upper CI:   0.8435
##          Weight:  16.5263

# es.type に "logit" と設定し、logOR を計算
esc_2x2(grp1yes = grp1yes, grp1no = grp1no,
              grp2yes = grp2yes, grp2no = grp2no,
              es.type = "logit")

## 
## Effect Size Calculation for Meta Analysis
## 
##      Conversion: 2x2 table (OR) to effect size logits
##     Effect Size:  -0.6523
##  Standard Error:   0.2460
##        Variance:   0.0605
##        Lower CI:  -1.1344
##        Upper CI:  -0.1701
##          Weight:  16.5263

リスク比の問題点であるゼロセルやダブルゼロ研究はオッズ比を計算するときにも同じように関係する (Chapter 3.3.2.1 参照)。しかし、オッズ比は RR に比べて、多くの人が理解しにくく、OR を RR と誤って解釈してしまうという欠点がある。

したがって、メタ分析ではリスク比のみを用いるか、結果を報告する際にオッズ比をリスク比に変換することが望ましい場合が多い (Julian Higgins et al. 2019, chap. 6.4.1.2)。この変換は以下の式で行うことが可能である (Zhang and Yu 1998)。(訳注:臨床論文でこれを行なっていることはほとんどない。)

\[\begin{equation} \text{RR} = \frac{\text{OR}}{\left(1-\dfrac{c}{n_{\text{control}}}\right)+ \left(\dfrac{c}{n_{\text{control}}}\times \text{OR} \right)} \tag{3.34} \end{equation}\]

R のオッズ比のメタ分析を行うには、以下の列をデータセットに含める必要がある。

event.e. 治療群・実験群におけるイベントの数。
n.e. 治療群・実験群のサンプルサイズ。
event.c. 対照群におけるイベントの数。
n.c. 対照群のサンプルサイズ。

3.3.3 発生率比

前に調べた二値アウトカムのデータに対する効果量、リスク比やオッズ比は、２つのグループのイベントの数を比較する方法である。しかし、これらのイベントが発生した時間は直接的には符号化されない。リスク比やオッズ比を計算するとき、両群の観察期間が同等であることを暗黙のうちに仮定している。さらに、リスク比とオッズ比は、イベントが発生するまでの時間に関する情報を提供しない。

時間軸がリサーチクエスチョンにそれほど関係しない場合、これでよいだろう。また、二値データが横断的で時間軸が全くない場合もある¹⁵。このような場合、リスク比やオッズ比は通常、適切な効果量の指標となる。

しかし、ここで、2つのグループの個人の10年間の死亡率を調べる研究を想像してみてみよう。この10年間に起こった出来事 (例えば、死亡) の数は、両群でほぼ同じである可能性がある。しかし、死亡がいつ起こったかを詳しく見てみると、一方の群では最初の数年間に多くのイベントが起こり、他方の群では10年間の観察期間の終わりまでやや多くのイベントが起こっていることがわかる。このデータから計算されるオッズまたはリスク比はおよそ1であり、群間差はないことを示す。しかし、これは重要なことを見逃している。一方のグループの参加者は、たとえ最終的に死亡したとしても、いくらか長く生存しているということである。

効果量の推定に時間を組み込むために、発生率比 (incidence rate ratio, IRR) を計算することができる。発生率比は、英語では単に rate ratio と呼ばれることもある。発生率比は、2つの発生率から構成されている。この発生率を計算するためには、まず人-時間の概念を理解する必要がある。

人-時間とは、研究参加者がイベントを起こす危険性があった時間の総和を表す。人-時間を計算するためには、すべての研究対象者のリスク時間 (日、週、年として表される) を合計する。しかし、リスク時間は人によって異なる。

例として、6人の被験者で研究を行う場合を考えてみよう。この研究は、ちょうど10年間続く。各年が終わるごとに、参加者にインタビューを行い、彼らがあるイベントを経験したかどうかを調べる。イベントが発生したことが確認された場合、その参加者の研究は終了し、研究が終了するまでその参加者を調査することはない。本研究の結果を図に示す。

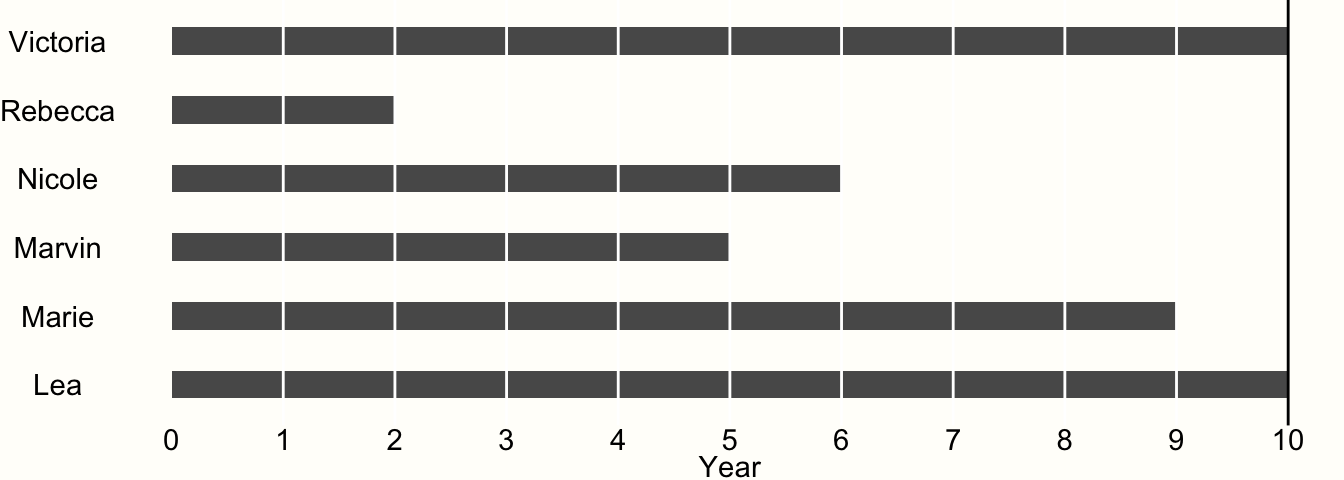
Figure 3.4: 時間-イベントデータの例

今回の参加者のうち、最後まで研究に参加したのは、Victoria と Lea の2人だけであることがわかる。これは、彼らが 10 年間の観察期間中、イベントを経験しなかったからである。したがって、両者とも 10 年間はアットリスク (訳注: リスクに曝されている状態、追跡中の状態のこと) であった。

他の参加者は全員、調査期間中にイベントを体験している。例えば、2 年目に Rebecca を調査したとき、彼女がその前の年にイベントを経験したことを発見した。しかし、私たちが知っているのは、その出来事が2年目に起こったということだけで、正確にはいつ起こったかわからないのである。

このような研究データは、区間打ち切りデータと呼ばれ、いわゆる生存解析を行う臨床試験で非常によく見受けられる。データが打ち切られているということは、レベッカが最終的にイベントを経験するまでにどれくらいの期間危険にさらされていたかを部分的にしか知らないということである。私たちは、彼女が1年目以降、2年目の終わりまでにイベントを経験したことを知っているが、それ以上のことは知ることはない。他の情報がないので、イベントが中間のどこかで発生したと仮定して、リスク時間を 1.5 年とすることにする。

打ち切られたデータ全てに同じ方式を適用すれば、この研究における人-年のリスクを計算することができる。

\[10 + 1.5+5.5+4.5+8.5+10 = 40\] すなわち、この研究での推定総人-年は40人年ということになる。1年は52週なので、この研究の人-週は $40 \times 52 = 2080$ と計算できる。

実験参加者年数がわかったので、これを $T$ とすると、1年以内の発生率も計算できる。調査期間中に4人の参加者がイベントを経験したことが分かっているので、イベントの数は $E=4$ となる。そして、この式で発生率 IR を計算することができる。

\[\begin{equation} \text{IR} = \frac{E}{T} \tag{3.34} \end{equation}\]

この例では、$4/40 = 0.1$ の発生率になる。この発生率は、1000人を1年間追跡調査した場合、100人がその間にそのイベントを経験することを意味する。

発生率比 (incidence rate ratio, IRR) を計算するためには、あるグループの発生率を他のグループの発生率で割る必要がある。

\[\begin{equation} \text{IRR} = \frac{ E_{\text{treat}}/T_{\text{treat}} }{E_{\text{control}}/T_{\text{control}}} \tag{3.35} \end{equation}\]

この式で、$E_{\text{treat}}$ と $T_{\text{treat}}$ は治療群のイベント数と人時、$E_{\text{control}}$ と $T_{\text{control}}$ は対照群のイベント数と人時である。もちろん、2つのグループは、例えば、女性と男性、喫煙者と非喫煙者など、関心のある他の二項対立変数を表すこともできる。

IRR は、リスク比やオッズ比と多くの特性を共有している。つまり、IRR は 1 を中心とし、マイナスになることはない。OR や RR と同様に、発生率比もメタ分析のために対数変換され、対数発生率比が作成される。

\[\begin{equation} \log \text{IRR} = \log_{e}(\text{IRR}) \tag{3.36} \end{equation}\]

これについては、次のように標準誤差を計算することが可能である (Rothman, Greenland, and Lash 2008, chap. 14)。

\[\begin{equation} SE_{\log \text{IRR}} = \sqrt{\frac{1}{E_{\text{treat}}}+\frac{1}{E_{\text{control}}}} \tag{3.37} \end{equation}\]

このように (対数) 発生率比と R の標準誤差を計算することができる。

# データを定義
e_treat <- 28    # 治療群のイベント数
e_contr <- 28    # 対照群のイベント数
t_treat <- 3025  # 治療群の Person-time
t_contr <- 2380  # 対照群の Person-time

# IRR を計算
irr <- (e_treat/t_treat)/(e_contr/t_contr)
irr

## [1] 0.7867769

# log-IRR を計算
log_irr <- log(irr)

# 標準誤差を計算
se_log_irr <- sqrt((1/e_treat)+(1/e_contr))

この例では、イベント数 $E_{\text{treat}}$ と $E_{\text{control}}$ が全く等しいが、治療群の方がリスクでの人時時間が長い場合をシミュレーションしている。この時間差は、IRR を計算するときに考慮される。したがって、得られる結果は1ではなく、IRR $\approx$ 0.79 となり、治療群の方が発生率が小さいことがわかる。

発生率比は、疫学や予防医学の研究でよく使われる。参加者を長期間にわたって追跡調査し、その間に定期的な評価を行う場合に使用することが可能である。しかし、実際には、メタ分析の一部として IRR を計算する際に考慮すべき注意点が1つある。すなわち、含まれる論文で報告された発生率データが十分に細かいことが重要である。論文では研究期間中のイベントの総数のみを報告し、その間の各評価ポイントで記録されたイベントの数は報告しないこともある。また、そもそも中間評価が行われていない可能性もある。

上記の例 (Figure 3.4 参照) では、参加者の危険にさらされている時間を推定するために、単純に、最後の「イベントのない」評価点とイベントが記録された評価点との間の中間点を取ることにする。これは、イベントがいつ起こったかの最良の推測に過ぎないということを心に留めておくことが重要である。中間点を取る場合でも、この例では、推定はまだ約半年ずれている可能性がある。

評価点間の時間をできるだけ小さくすれば、人-時推定値は最適になる。研究の評価間隔が粗すぎるかどうかはメタ分析の文脈に依存する。ただし、そのような感度分析を行うことは常に推奨される (Panageas et al. 2007)。

これは、異なる人-時推定値に基づく研究の IRR を再計算することを意味する。

インターバルの中点を使用し
最後の「イベントのない」評価ポイントを使用し
イベントが検出された評価ポイントを使用している。

これらの3つのメタ分析の結果がすべて同じ方向を向いていれば、より確信を持って調査結果を公表することが可能である。また、評価期間が研究間であまりに異ならないことを確認する必要がある (例えば、ある研究では毎日イベントを調査し、他の研究では年１回だけ調査する)。メタ分析での IRR の適用性に疑問がある場合、代わりに (または追加で) リスク比またはオッズ比を計算する可能性が常に存在する。ただし、この場合、評価時点が (1 年後など) 各研究で類似していることを確認する必要がある。

R の発生率比に基づくメタ分析を計算するためには、データセットに以下の列を用意する必要がある。

event.e: 治療群・実験群におけるイベント総数。
time.e: 治療群・実験群における人-時 (person-time)。全ての研究で人-時の単位 (人-日、人-週、人-年) を統一して表記する。
event.c: 対照群におけるイベント総数。
time.c: 対照群における人-時 (person-time)。全ての研究で人-時の単位 (人-日、人-週、人-年) を統一して表記する。

ハザード比と発生率比の限界

発生率や IRR は、事象データやその事象が発生する時間帯を要約する直感的な方法である。しかし、欠点がないわけではない。発生率を計算するためには、母集団における基礎となるリスクが時間と共に一定であると仮定する (例えば、研究の1年目と2年目の間など)。IRRでは、基礎となるリスクは治療群と対照群で異なるかもしれないが (例えば、治療が事象を経験するリスクを減らすため)、各群内 (within) のリスクは一定であると仮定する。

この仮定が非常に単純であることは容易に理解できる。イベントリスクが時間とともに変化しないと仮定することが非常に非現実的なシナリオは多い (Kraemer 2009, 例: 転移性癌患者の死亡)。Bender and Beckmann (2019) は、シミュレーション研究に基づいて、IRRの使用は、両群の平均観察期間が大きく異ならないとき、および調査対象イベントのベースラインリスクが比較的低い (25%未満) 場合にのみ適切であると結論づけている。

時間-事象データに基づく群間差を表現する代替指標として望ましいのがハザード比 (HR) である。ハザード比は、2つの (比例する) ハザード関数の比で、ある時点 $t$ である事象を経験することの (変化する) 瞬間的なリスク (これを、「ハザード」と言う) を記述している。

ハザード比は、一般的に Cox 回帰モデルを用いて、個々の参加者データを基に推定される。すべての研究から対数ハザード比 $\log_{\text{e}}(\text{HR})$ とそれに対応する標準誤差を抽出できれば、逆変量プーリング を用いたメタアナリシスを行うことができる (Chapter 4.1.1 参照)。これは、例えば対数リスクやオッズ比をプールするのと同じように機能する。 R では、対数ハザード比のプーリングは metagen 関数で、sm 引数を "HR" に設定して行う (Chapter 4.2.1 参照)。

すべての研究が (対数) ハザード比とその標準誤差を報告しているわけではないので、HR をプールすることは実際には大変な問題になることもある。Parmar, Torri, and Stewart (1998) は、特に log-rank test の結果や 生存曲線 から対数ハザード比とその分散を導き出す様々な方法について説明している。この方法は手間がかかるが、報告されたデータから IRR を導出する方法も間違いなく手間がかかる。

3.4 効果量補正

ある研究 $k$ に対して計算した効果量 $\hat\theta_k$ はその研究の真の効果量 $\theta_k$ の推定値であり、サンプル誤差 $\epsilon_k$ により $\hat\theta_k$ は $\theta_k$ から乖離すると、Chapter 3.1 では取り上げた。残念ながら、多くの場合、これは過度の単純化である。先ほどの式では、推定された効果量と真の効果量を分けるのは、サンプル誤差だけである。式に従えば、サンプル誤差が小さくなれば、効果量の推定値は母集団における真の効果量に「自然に」収束していく。

しかし、効果量の推定に系統的な誤差、すなわちバイアスが加わると、この限りではない。このようなバイアスは、さまざまな理由がある。効果量指標の数学的特性そのものに起因するものもあれば、研究の実施方法によって生じるバイアスもある。

研究の進め方に起因するバイアスに対しては、バイアスの危険性を評価することで対応可能である (バイアスの危険性評価ツールの紹介は Chapter 1.4.5、バイアスの危険性の可視化方法は Chapter 15 を参照)。この判断は、例えばサブグループ解析において、バイアスリスクがプールされた効果の違いに関連しているかどうかを判断するためにも使用可能である (Chapter 7)。

効果量の統計的性質に起因するバイアスに対処するために、メタ解析を始める前に、特定の効果量補正手法を用いてデータを調整することが可能である。

この章では、よく使われる3つの効果量補正の方法と、それらを R でどのように実装するかを説明する。

3.4.1 スモールサンプルバイアス

標準化平均差 (SMD) は、2群の連続したアウトカムデータがある場合に計算できる効果量である。しかし、標準化平均差は、研究のサンプルサイズが小さいとき、特に $n \leq$ 20 (L. V. Hedges (1981)) のとき、上方バイアス (upward bias) を持つことが分かっている。このサンプルサイズが小さいというバイアスは、研究のサンプルサイズが小さい場合、SMD が系統的に真の効果量を過大評価することを意味する。

そこで、すべての研究の標準化平均差をスモールサンプルバイアスで補正し、Hedges’ $g$ と呼ばれる効果量を算出することが賢明である。Hedges’ $g$ はこの補正の考案者である Larry Hedges にちなんで名づけられた。未補正の SMD/Cohen’s $d$ を Hedges’ $g$ に変換する式は次のようになる。

\[\begin{equation} g = \text{SMD} \times (1-\frac{3}{4n-9}) \tag{3.38} \end{equation}\]

この式で、$n$ は研究の総サンプルサイズを表す。標準化されていない SMD/Cohen’s $d$ を Hedges’ $g$ に変換するには、{esc} パッケージの hedges_g 関数を使うと簡単に可能である。

# esc パッケージをロード
library(esc)

# 未補正 SMD とサンプルサイズ n を定義
SMD <- 0.5
n <- 30

# Hedges g に変換
g <- hedges_g(SMD, n)
g

## [1] 0.4864865

出力でわかるように、Hedges’ $g$ は未補正の SMD より小さくなっている。Hedges’ $g$ は補正前の SMD より大きくなることはなく、サンプルサイズが小さいほど2つの指標の差は大きくなる (Figure 3.5参照)。

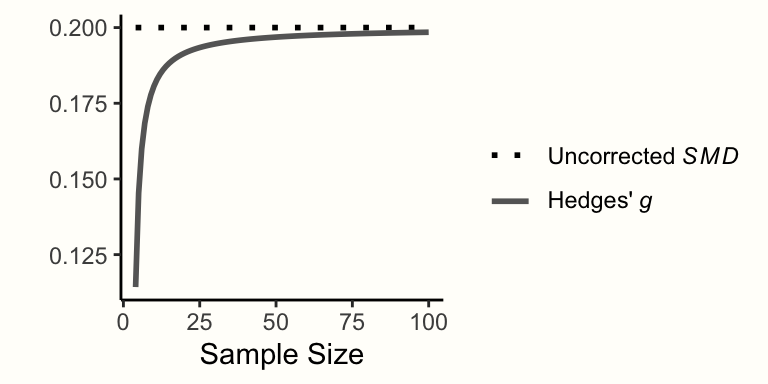
Figure 3.5: サンプルサイズを変化させた時の未補正 SMD 0.2 と補正済み SMD 値

ここで重要なことは、SMD と Hedges’ $g$ という用語が研究報告で同じように使われることがあることである。ある研究が SMD として結果を報告している場合、著者が本当に未補正の標準化平均差を指しているのか、それとも小サンプルバイアス補正が適用されているのか (つまり Hedges’ $g$ が使われているのか) を確認することが適切である。

3.4.2 非信頼性

測定誤差のために効果量の推定値にバイアスがある可能性もある。ほとんどのアンケートやテストは、興味のある結果を完璧に測定することはできない。測定誤差が生じにくい測定器 (訳注: instrument、測定器と訳したが質問紙なども含まれる) ほど、信頼性が高いと言える。ある変数 $x$ を測定する測定器の信頼性は、信頼性係数 $r_{xx}$ で表すことができ、0から1の間の値をとることができる。信頼性はしばしばテスト・再テスト信頼性と定義され、同一人物を同じような状況で短期間に2回以上測定し、その値の相関を計算することで求められる¹⁶。

2つの連続変数の関係を調べるとき、これらの変数を評価するために使用される調査測定器の一方または両方に信頼性が欠けていると、減衰 (attenuation) と呼ばれる現象が起こることがある。この問題は、1904年に有名な心理学者 Charles Spearman (1904) によって早くも記述されている。例えば、相関を計算するときに、片方または両方の変数に誤差があると、真の相関を過小評価することになる。相関は希釈されるのである。しかし、良いニュースもある。もし、測定の (非) 信頼性の推定値があれば、真の効果の大きさをより良く推定するために、この減衰を補正することが可能なのである。

John Hunter and Frank Schmidt は、メタ分析の分野で重要な貢献者であり、メタ分析の一部として減衰の補正を行う方法を開発し推進している (Hunter and Schmidt 2004, chap. 3 と Chapter 7)。この補正は他のいくつかの手法の一つであり、これらをまとめて「Hunter and Schmidt techniques」または「Hunter and Schmidt 法」と呼ぶこともある (Hough and Hall 1994)。

Hunter and Schmidt の減衰補正は、(積率) 相関と標準化平均差に適用することができる。まず、メタ解析の一環として研究の積率相関 $r_{xy}$ を計算する際に、変数 $x$ の測定における信頼性の低さを補正したいと仮定する。$r_{xx}$ で示される $x$ の測定の信頼性がわかれば、相関の補正版である ${r_{xy}}_{c}$ を計算することが可能である。

\[\begin{equation} {r_{xy}}_{c} = \frac{r_{xy}}{\sqrt{r_{xx}}} \tag{3.39} \end{equation}\]

アウトカム $x$ が2群で観測され、その群間の標準化平均差を計算することが目的である場合、同様の方法で補正を行い、$\text{SMD}_c$を得ることができる。

\[\begin{equation} \text{SMD}_c = \frac{\text{SMD}}{\sqrt{r_{xx}}} \tag{3.40} \end{equation}\]

二つの連続変数 $x$ と $y$ を用いて積率相関を計算するとき、$y$ の信頼性係数 $r_{yy}$ もわかっていれば、$x$ と $y$ の両方の信頼性の低さを補正することも可能である。

\[\begin{equation} {r_{xy}}_{c} = \frac{r_{xy}}{\sqrt{r_{xx}}\sqrt{r_{yy}}} \tag{3.41} \end{equation}\]

最後に、標準誤差の補正も必要である。標準誤差の補正は、効果量そのものと同じ方法で行いる。1つの変数 $x$ を補正する場合は、以下の式で計算可能である。

\[\begin{equation} SE_c = \frac{SE}{\sqrt{r_{xx}}} \tag{3.42} \end{equation}\]

$x$ と $y$ の両方について補正 (積率相関) したい場合は、以下の式が使える。

\[\begin{equation} SE_c = \frac{SE}{\sqrt{r_{xx}}\sqrt{r_{yy}}} \tag{3.43} \end{equation}\]

相関やSMDを補正した後、${r_{xy}}_c$ を Fisher’s $z$ に変換したり(Chapter 3.2.3) $\text{SMD}_c$ を Hedges’ $g$ に変換するなど(Chapter 3.4.1)、一般的な変換を適用することが可能である。

ここでは、 R を使った例で補正方法を試してみよう。

# 未補正の相関と SMD とその標準誤差を定義
r_xy <- 0.34
se_r_xy <- 0.09
smd <- 0.65
se_smd <- 0.18

# xとyの信頼性を定義
r_xx <- 0.8
r_yy <- 0.7

# x の信頼性の低さを考慮して SMD を補正
smd_c <- smd/sqrt(r_xx)
smd_c

## [1] 0.7267221

se_c <- se_smd/sqrt(r_xx)
se_c

## [1] 0.2012461

# x と y の信頼性の低さを考慮して相関を補正
r_xy_c <- r_xy/(sqrt(r_xx)*sqrt(r_yy))
r_xy_c

## [1] 0.4543441

se_c <- se_r_xy/(sqrt(r_xx)*sqrt(r_yy))
se_c

## [1] 0.1202676

この例の結果を詳しく見ていこう。補正により、相関と SMD が補正前の初期値より大きくなっていることがわかる。しかし、標準誤差が大きくなっていることもわかる。この結果は意図的なもので、標準誤差を補正することで、データに想定される測定誤差を取り込むことができるのである。

組織心理学など一部の分野では、減衰補正を適用することが一般的である。しかし、生物医学分野を含む他の分野では、この手順はほとんど使用されていない。メタ分析では、各研究で信頼性係数 $r_{xx}$ (および $r_{yy}$) が報告されている場合のみ、信頼性の低さに対する補正を実行することが可能である。

信頼性係数が報告されていない場合も非常に多い。このような場合、先行研究に基づく測定器の信頼性の値を仮定することがある。しかし、補正が効果量の値に大きな影響を与えることを考えると、$r_{xx}$ の推定値が不適切だと、結果がかなり歪んでしまう。また、メタ分析において、一部の効果量だけを補正し、他の効果量を補正しないようにすることは不可能である。これらの理由により、残念ながら信頼性補正の適用範囲は実際には限定されることが多い。

3.4.3 範囲指定

Hunter and Schmidt (2004, chap. 3 と Chapter 7) によって提案されたもう一つの効果量調整は、範囲制限の問題を扱うものである。範囲制限とは、ある変数 $x$ の変動が、興味のある実際の母集団よりも研究で小さいときに起こる現象である。これは、母集団全体を代表していない可能性のある個体から非常に選択的にサンプルを採取した場合によく起こる。

例えば、ある研究で、被験者の年齢と認知機能の相関が報告された場合を考えてみよう。直感的には、これらの変数には確かに相関があると考えるだろう。しかし、65歳から69歳の参加者だけを対象とした研究であれば、この2つの変数の間に (高い) 相関が見られる可能性は極めて低い。これは、調査サンプルの年齢が非常に限定されているためである。年齢には実際の変動がないため、この変数は認知能力の良い予測因子にはなり得ないということである。

測定器の信頼性の低さ (前章参照) と同様、これは研究の効果を人為的に減衰させることにつながる。実際には重要な関連がある場合でも、それを検出することができない。

SMD や相関 $r_{xy}$ の範囲制限を補正することは可能である。ただし、そのためには、対象母集団の無制限標準偏差 $s_{\text{unrestricted}}$ を知っている (または推定している) ことが必要である。興味のある母集団は、メタ分析のリサーチクエスチョンによって決定される。

例えば、高齢者における年齢と認知機能の関係を調べたい場合、65歳以上の高齢者 (一般的に研究において「高齢者」はこのように定義される) の大規模代表サンプルにおける標準偏差の推定値を検索することが考えられる。もちろん、これは範囲限定であるが、メタ分析で扱う研究集団を反映しているため、年齢を重要な範囲に限定している。

範囲制限を補正するためには、制限されていない母集団の標準偏差 $s_{\text{unrestricted}}$ と、本研究で制限した変数の標準偏差 $s_{\text{restricted}}$ の比である $U$ を計算する必要がある。

\[\begin{equation} U = \frac{s_{\text{unrestricted}}}{s_{\text{restricted}}} \tag{3.44} \end{equation}\]

$s_{\text{unrestricted}}$ の値は、例えば、興味のある変数を評価した過去の代表的な研究から得ることができる。そして、$U$ を用いて、この式で相関の値 $r_{xy}$ を補正することができる。

\[\begin{equation} {r_{xy}}_c = \frac{U\times r_{xy}}{\sqrt{(U^2-1)r_{xy}^2+1}} \tag{3.45} \end{equation}\]

これにより、補正後の相関 ${r_{xy}}_c$ を求めることができる。また、同じ式で SMD の補正版も計算できる。

\[\begin{equation} \text{SMD}_c = \frac{U\times \text{SMD}}{\sqrt{(U^2-1)\text{SMD}^2+1}} \tag{3.46} \end{equation}\]

また、$r_{xy}$とSMDの標準誤差も、それぞれこれらの式で補正する必要がある。

\[\begin{equation} SE_{{r_{xy}}_c} = \frac{{r_{xy}}_c}{r_{xy}}SE_{r_{xy}} \tag{3.47} \end{equation}\]

\[\begin{equation} SE_{{\text{SMD}}_c} = \frac{{\text{SMD}}_c}{\text{SMD}}SE_{\text{SMD}} \tag{3.48} \end{equation}\]

相関やSMDを補正した後、${r_{xy}}_c$ を Fisher’s $z$ に変換したり (Chapter 3.2.3.1 )、$\text{SMD}_c$ を Hedges’ $g$ に変換するなど (Chapter 3.4.1 )、よくある変換を行うことができるようになっている。では、 R を使った補正を試してみよう。

# 補正するための相関関係を定義
r_xy <- 0.34
se_r_xy <- 0.09

# 指定 SD と非制限 SD を定義
sd_restricted <- 11
sd_unrestricted <- 18

# U を計算
U <- sd_unrestricted/sd_restricted

# 相関を補正
r_xy_c <- (U*r_xy)/sqrt((U^2-1)*r_xy^2+1)
r_xy_c

## [1] 0.5091754

# 標準誤差を補正
se_r_xy_c <- (r_xy_c/r_xy)*se_r_xy
se_r_xy_c

## [1] 0.1347817

他の Hunter and Schmidt の調整と同様に、範囲制限の補正は、他の研究分野よりもある研究分野でより一般的に見られるものである。範囲制限の補正を適用する場合、メタ分析におけるすべての効果量に対して補正を実行することが重要である。技術的には、すべてのメタ分析で範囲制限の補正を行うことは可能であるが、多くの場合、これは必要ではない。

実際には、各研究がメタ分析の範囲を完全に表現していることはほとんどない。実際、メタ分析の目的は、個々の研究の結果を超えることである。したがって、範囲制限の補正は、いくつかの研究の範囲が大きく制限されている場合にのみ必要となる場合がある。

更なる学習

このガイドでは、信頼性の低さと範囲制限に関する補正のみを取り上げる。なぜなら、これらの問題は実際に最もよく見られるからである。しかし、Hunter and Schmidt は、他にも様々な種類の誤差補正を提案している。いくつかの追加手法とともに、この手法は、心理測定メタ分析 (psychometric meta-analysis) と呼ばれることもある。

Hunter and Schmidt の方法について詳しく知りたい方は、彼らの著書である Methods of Meta-Analysis (Hunter and Schmidt 2004) がわかりやすく、包括的な概要を提供しているので、参照されたい。Borenstein et al. (2011) の38章にも、短い紹介がある。

Hunter and Schmidt の手法の多くは、{psychmeta} (Dahlke and Wiernik 2019) と呼ばれる R パッケージにも実装されている。

3.5 よくある問題

この章では、効果量を計算する際に、実際によく直面する問題にもう少し時間を割きたいと思いる。まず、効果量のデータが異なる形式で報告されている場合にどうすればよいかを説明する。その後、後のステップでメタ解析のプーリングに影響を与える解析単位の問題を検討する。

3.5.1 効果量のデータ形式が異なる

前の章で効果量の計測方法について説明したとき、データセットの列として必要な変数の種類についても触れた。これらの変数は、 R 関数が効果量を計算し、メタ分析を実行するために必要である。例えば、群間標準化平均差のメタ分析を計算するためには、両群の平均値、標準偏差、サンプルサイズを準備する必要がある。

すべての研究からこの情報を抽出することができれば、すべてがうまくいく。しかし、実際には、すべての研究が適切な形式で結果を報告しているわけではないことにすぐに気がつくだろう。例えば、2群の生データを報告せず、標準化平均差の計算値とその信頼区間だけを報告する研究もある。また、2群間の差を調べる$t$-検定や分散分析 (ANOVA) の結果のみを報告する研究もある。

このような場合、メタ分析に生の効果量データを使うことができなくなることがよくある。その代わりに、各研究の効果量をあらかじめ計算して、それをプールする必要がある。メタ分析に最低限必要な情報は、研究の効果量と標準誤差であることは、Chapter 3.1 ですでに確認した。したがって、結果を効果量と標準誤差の推定値に変換することができれば、その研究を取り入れることができるのである。Chapter 17 では、他のタイプの報告データから効果量を導き出すのに役立つ効果量コンバータをいくつか紹介している。

しかし、これらのツールを使っても、効果量が算出できない研究がある可能性がある。そのような場合に残された方法としては、「研究選択」の章で述べたように、それぞれの論文の著者に何度も連絡を取り、効果量を算出するために必要なデータを提供してもらえないかお願いすることである。それでもダメなら、その研究は除外するしかない。

Chapter 4.2.1 では、 R の特殊な関数である metagen について学ぶ。この関数を使うと、事前に計算された効果量のデータをメタ分析することが可能である。この関数を使うには、データセットに以下の列を用意する必要がある。

TE. 各研究の効果量の計算値。
seTE. 各効果量の標準誤差。

3.5.2 分析単位問題

メタ分析において、1つの研究が2つ以上の効果量に寄与することは珍しいことではない。特に、(1)ある研究が2つ以上のグループを含んでいる、(2)ある研究が2つ以上の道具を使って結果を測定している、などの場合がある。どちらの場合も問題がある。メタ分析において、研究が複数の効果量に寄与する場合、メタ分析における各効果量は独立であるという中核的な仮定の1つに違反することになる (Julian Higgins et al. 2019, chap. 6.2 と Chapter 23; Borenstein et al. 2011, chap. 25)。この仮定が満たされない場合、分析単位 (unit of analysis) の問題を扱っていることになる。

例えば、治療 A を検査する群、治療 B を投与する群、そして対照群 C がある。この研究では、2個の効果量を計算することが可能である。結果のデータによって、これらはリスク比、オッズ比、または発生率比、あるいは標準化平均差になる。治療 A と対照を比較する効果量 $\hat\theta_{\text{A-C}}$ と、治療 B と対照を比較する効果量 $\hat\theta_{\text{B-C}}$ の2つがある。$\hat\theta_{\text{A-C}}$ と $\hat\theta_{\text{B-C}}$ の両方を同じメタ分析に含めると、C の情報が2回含まれているため、これらの効果量は独立したものではない。この問題は、二重カウントとも呼ばれる。

C を二重カウントしたため、2つの効果量は相関がある。サンプルサイズが全群で等しい場合、この相関は $r =$ 0.5 であることがわかる (Borenstein et al. 2011, chap. 25)。これは、A と B が独立した群であるため、相関がないためである。しかし、両方の効果量における対照群は同一であるため、完全な相関は 1 となり、その中点は 0.5 となる。群の二重カウントは、影響を受ける効果量の精度 (すなわち、標準誤差) を過大評価することになる。これは、メタ分析でこれらの効果に与える重みを増大させ、最終的に結果を歪めることになる。この問題に対処するために、3つの方法がある。

共有群のサンプルサイズを分割する。これは、効果量を計算するときに、C 群のサンプルサイズ (例えば $n =$ 200) を A との比較と C との比較で均等に分けることを意味する。二値結果のデータを扱う場合は、イベントの数も均等に分割する。この例では、先ほどと同じように2つの効果量を計算したが、今度は C が両方の計算で 100 人のみで構成されているように見せかける。このアプローチにより、効果量の精度がダブルカウントのために人為的に高くなるという問題が解決される。しかし、効果量が相関したままなので、まだ最適とは言えない (Julian Higgins et al. 2019, 23.3.4)。
群を削除する。非常に腕力を使う手法は、単純に1つの比較、例えば $\hat\theta_{\text{B-C}}$ をメタ分析から完全に削除することである。これは分析単位の問題を解決するものの、新たな問題を引き起こす。効果量を1つ捨てるだけだと、関連する可能性のある情報を失ってしまうのである。
群を合体する。この手法は、2つの群の結果を組み合わせて、1つの比較しか残らないようにするものである。この例では、A と B のデータを組み合わせて、プールした結果を C と比較することを意味する。これは、両群の参加者数とイベント数を合計すればよい二値アウトカムデータでは比較的簡単なことである。しかし、平均値や標準偏差のような連続的なデータでは、少し複雑になる。「各種ツール」の Chapter 17.9 には、このようなデータを結合するための R 関数がある。群を合体することで、二重カウントや効果量の相関を回避することが可能である。そのため、この方法はコクランでも推奨されている (Julian Higgins et al. 2019, chap. 23.3.4)。とはいえ、この方法にも欠点がある。2 群があまりにも異なり、実際には比較できないものを一緒にしてしまう可能性があるのである。A は最先端の介入、B はエビデンスベースの乏しい時代遅れのアプローチでなど、A 群と B 群の治療がまったく異なることもある。この 2 つの治療を組み合わせても効果が見られない場合、これが両方のタイプの介入に当てはまるのか、B の効果のなさが単に A の効果を希釈したのかを切り分けるのはほぼ不可能である。したがって、アプローチ (1) と (2) は、2 群があまりにも異質な場合に使用される。

分析単位の問題は、ある研究が複数の測定器を用いて結果を測定した場合にも発生する。これは、解析したい変数をどのように選ぶべきかを決定する明確な「ゴールド・スタンダード」がない場合によくあることである。これらの測定のそれぞれについて効果量を計算しメタ分析に含めると、二重カウントになってしまう。さらに、効果の測定に同じサンプルが使用されるため、効果量には相関がある。この状況に対処するためには、3つのアプローチがある。

まず、単純に1つの研究につき1つの測定器を選択する方法である。この選択は、体系的かつ再現可能な方法で行うことが重要である。できることといえば、解析計画書 (Chapter 1.4.2) において、メタ解析のための測定器の階層を定義しておくくらいである。この階層は、特定の測定器の信頼性に関する過去の証拠に基づくことも、どのタイプの測定器が研究課題の内容を最もよく反映しているかに基づくこともできる。そして、この階層によって、複数の測定器が利用可能な場合に、どの測定器を選択するかを明確に決定する。
また、計算された効果量を用いてそれらを集約し、各研究が1つの効果量 (集約されたもの) しか提供しないようにすることも可能である。これはやや「総当り」的なアプローチである。この場合、効果量が研究内でどの程度強く相関しているかを特定する必要があるが、この値は通常知られていない。Chapter 17.10 では、あらかじめ計算された効果量を、各研究について1つの推定値に集約できる関数を紹介する。
第三のアプローチは、利用可能なすべての測定器からのデータを含み、メタ分析において研究が1つ以上の効果量に寄与するという事実を説明できるメタ分析モデルを使用することである。これは「3 レベル」メタ分析モデルによって実現されるもので、Chapter 10 で検討する。

\[\tag*{$\blacksquare$}\]

3.6 演習問題

知識を試そう！

効果量という言葉に明確な定義はあるか？人々は、効果量という言葉で何を指すか？

観測された効果量が母集団の真の効果量から乖離する主な理由を挙げなさい。それはどのように定量化できるのか。

なぜ大規模な研究は小規模な研究よりも真の効果の推定に優れているのか？

効果量の指標は、どのような基準を満たせばメタ分析に使えるのか？

標準化平均差 (Standardized Mean Difference, SMD) が1であることは何を表しているのか？

比 (オッズ比など) に基づく効果量をプールするためには、どのような変換が必要か。

効果量補正の種類を3つ挙げよ。

分析単位の問題はどのような場合に発生するか？どうすれば回避できるか？

問題の解答は、本書の巻末 Appendix A にある。

3.7 概要

効果量は、メタ分析の構成要素である。メタ分析を行うには、少なくとも効果量とその標準誤差の推定値が必要である。
効果量の標準誤差は、その研究による効果量の推定がどれだけ正確であるかを表している。メタ分析では、精度の高い効果量は、真の効果をより良く推定できるため、より高い重みが与えられる。
メタ分析で使用する効果量には様々なものがある。一般的なものは、「1 変数」の関係尺度 (平均や割合など)、相関、(標準化) 平均差、そしてリスク比、オッズ比、発生率比などである。
効果量には、測定誤差や範囲制限などによるバイアスが生じることがある。標準化平均差の小サンプルバイアス、信頼性の低さによる減衰、範囲制限の問題など、いくつかのバイアスを補正する公式がある。
その他のよくある問題としては、効果量を計算するために必要なデータを異なる形式で報告している研究、また、複数の効果量を報告している研究で生じる分析単位の問題などがある。

2 R の発見

4 効果量のプール

	Event	No Event
Treatment	\(a\)	\(b\)	\(n_{\text{treat}}\)
Control	\(c\)	\(d\)	\(n_{\text{control}}\)
	\(n_E\)	\(n_{\neg E}\)