14 検出力分析

メ タ分析が有用な理由の一つは、不正確な知見を複数組み合わせて、より正確な知見を得ることができるためである。ほとんどの場合、メタ分析は、含まれるどの研究よりも狭い信頼区間を持つ推定値を生成する。これは、真の効果が小さい場合に特に有効である。一次研究では小さな効果の有意性を確認できないだろうが、メタ分析による推定値は、そのような小さな効果が存在することを確認するために必要な統計的検出力を提供できることが多いのである。
しかし、統計的検出力の不足は、メタ分析においてさえも重要な役割を果たすことがある。多くのメタ分析で含まれる研究の数は少なく、\(K =\) 10 件以下であることが多い。例えば、コクランのシステマティックレビューにおける研究の数の中央値は6である (Borenstein et al. 2011)。メタ分析にはサブグループ分析やメタ回帰が含まれることが多く、その場合はさらに検出力が必要となることを考慮すると、この問題はさらに深刻になる。さらに、多くのメタ分析では、研究間の異質性が高い。これもまた全体的な精度を低下させ、結果として統計的検出力を低下させる。
統計的検出力の概念については、Chapter 9.2.2.2 ですでに触れ、p-曲線法について学んだ。統計的検出力の背後にある考え方は、古典的な仮説検定に由来している。これは仮説検定で起こりうる2種類のエラーに直接関係している。最初のエラーは、帰無仮説 (\(\mu_1 = \mu_2\)) が真であるのに、対立仮説 (\(\mu_1 \neq \mu_2\)) を受け入れることである。これは、タイプ I または \(\alpha\) エラーとしても知られている。逆に、対立仮説が真であるのに、帰無仮説を受け入れることもある。これは、タイプ II または \(\beta\) エラーとして知られている偽陰性 (false negative) を発生させる。
検定の検出力は、\(\beta\) に直接依存し、検出力 = \(1 - \beta\) と定義される。帰無仮説では、2群の平均の間に差がないと仮定し、対立仮説では差 (すなわち「効果」) が存在すると仮定する。統計的検出力は、効果 (つまり、平均値の差) が存在する場合に、検定がそれを検出する確率として定義できる。
\[\begin{equation} \text{Power} = P(\text{reject H}_0~|~\mu_1 \neq \mu_2) = 1 - \beta \tag{14.1} \end{equation}\]
タイプ I の誤りはタイプ II の誤りよりも重大であると考えるのが一般的である。したがって、\(\alpha\) レベルは慣習的に 0.05 に設定され、\(\beta\) レベルは 0.2 に設定されている。つまり、\(1-\beta\) = 1 - 0.2 = 80% という閾値をもたらし、通常、検定の統計的検出力が適切かどうかを決定するのに使われる。研究者が新しい研究を計画するとき、通常、80% の検出力が保証されるサンプルサイズを選択する。真の効果が大きければ、統計的に有意な結果を得ることは容易である。したがって、検出力が 80% に固定されている場合、必要なサンプルサイズは真の効果の大きさにのみ依存する。想定される効果が小さいほど、80% の検出力を確保するために必要なサンプルサイズは大きくなる。
一次研究を行う研究者は、発見されると予想される効果量に基づいて、a priori に、サンプルのサイズを計画することができる。メタ分析では公表されたものしか扱えないため、状況は異なる。しかし、メタ分析に含める研究の数や種類については、ある程度コントロールすることができる (例えば、より緩やかな、あるいは厳しい包含基準を定義する)。こうすることで、全体の検出力を調整することもできる。メタ分析における統計的検出力に影響を与える要因はいくつかある。
対象研究の総数とそのサンプルサイズ。どれくらいの数の研究を見込んでいるのか、またその数は少ないのか多いのか。
見つけたい効果量。これは特に重要で、効果量がどの程度大きければ意味があるのかを仮定しなければならないことがある。例えば、あるうつ病の介入研究では、SMD = 0.24 という小さい効果でも患者にとって意味がある可能性があると計算されている (Pim Cuijpers et al. 2014)。介入の負の効果 (例えば、死亡や症状の悪化) を研究したい場合、非常に小さな効果量であっても極めて重要であり、検出されるべきものである。
予想される研究間の異質性。異質性が大きいとメタ分析による推定値の精度と、その結果、有意な効果を見出す可能性にも影響する。
上記以外にも、サブグループ分析など、実施したい分析について考えることも重要である。各サブグループにはどれくらいの研究があるのか?各グループでどのような効果を見出したいのか?
Post-Hoc 検出力検定: 「検出力の乱用」
検出力分析は、必ず a priori、つまりメタ分析を実行する前に行わなければならない。
分析の後に行われる検出力分析 (「post hoc 分析」) は、深い欠陥のある論理に基づいている (Hoenig and Heisey 2001) 。まず、post hoc の検出力分析は、一様であり、まだ知らないことは何も教えてくれない。収集したサンプルに基づいて効果が有意でないことがわかったとき、計算された post hoc 検出力は、定義上、不十分 (すなわち、50% 以下) である。あるテストの post hoc に検出力を計算するとき、単に結果の \(p\) 値に直接リンクしている検出力関数で「遊んで」いるにすぎない。
post-hoc の検出力の推定値には、\(p\) 値がまだ教えてくれていないことはない。すなわち、検定の効果とサンプルサイズに基づいて、検出力が統計的有意性を確認するのに不十分であることを示している。
post hoc に検出力を解釈すると、power approach paradox (PAP) にもつながる。このパラドックスは、有意な効果をもたらさない分析では、p値が小さいと、帰無仮説が真であるというより多くの証拠を示すと考えられ、真の効果を検出する力が高くなるために生じる。
14.1 固定効果モデル
固定効果モデルの下でのメタ分析の検出力を決定するために、対立仮説が正しいことを表す分布を指定しなければならない。しかし、これを行うには、単に \(\theta \neq 0\) (すなわち、何らかの効果が存在する) というだけでは不十分である。十分な検出力 (80%) で検出したい特定の真の効果を仮定しなければならない。例えば、SMD = 0.29 である。
効果量をその標準誤差で割ると \(z\) スコアになることは、以前すでに取り上げた (Chapter 8.1.2 を参照)。\(z\) スコアは、標準正規分布に従う。ここで、\(|z| \geq\) 1.96 という値は、効果がゼロとは有意に異なることを意味する (\(p<\) 0.05)。これはまさにメタ分析で達成したいことである。つまり、結果の正確な効果量と標準誤差がどんなに大きくても、\(|z|\) の値は少なくとも 1.96 でなければならず、したがって統計的に有意でなければならない。
\[\begin{equation} z = \frac{\theta}{\sigma_{\theta}}~~~\text{where}~~~|z| \geq 1.96. \tag{14.2} \end{equation}\]
プール効果量の標準誤差である \(\sigma_{\theta}\) (「シグマ・シータ」と読む) の値は、以下の式を用いて計算することができる。
\[\begin{equation} \sigma_{\theta}=\sqrt{\frac{\left(\frac{n_1+n_2}{n_1n_2}\right)+\left(\frac{\theta^2}{2(n_1+n_2)}\right)}{K}} \tag{14.3} \end{equation}\]
ここで、\(n_1\) と \(n_2\) は、ある研究のグループ 1 とグループ 2 のサンプルサイズを表し、\(\theta\) は、想定される効果量 (標準化平均差を表している)、\(K\) は、メタ分析における研究の総数である。簡略化のため、この式は、含まれるすべての研究において、両群のサンプルサイズが等しいと仮定している。
この式は、標準化平均差の標準誤差を計算するのに使われる式と非常によく似ているが、1 つだけ例外がある。ここで、標準誤差を \(K\) で割る。これは、プール効果標準誤差が、メタ分析における研究の総数を表す係数 \(K\) によって減少することを意味する。言い換えれば、固定効果モデルを仮定した場合、研究をプールすると、全体効果の精度が \(K\)-倍になる72。
\(\theta\) を定義し、\(K\) を計算した結果、\(z\) という値になる。この \(z\) スコアは、群サイズ \(n_1\) と \(n_2\) を持つ \(K\) 件の研究がある場合、メタ分析の検出力を得るために使用することができる。
\[\begin{align} \text{Power} &= 1-\beta \notag \\ &= 1-\Phi(c_{\alpha}-z)+\Phi(-c_{\alpha}-z) \notag \\ &= 1-\Phi(1.96-z)+\Phi(-1.96-z). \tag{14.4} \end{align}\]
ここで、\(c_{\alpha}\) は、指定された \(\alpha\) レベルが与えられたときの、標準正規分布の臨界値である。記号 \(\Phi\) (「ファイ」と読む) は、標準正規分布の累積分布関数 (cumulative distribution function, CDF) である \(\Phi(z)\) を表す。 R では、標準正規分布の CDF は pnorm 関数で実装されている。
この公式は、固定効果メタ分析の検出力を計算するために使用できる。\(K =\) 10 件の研究があり、両群がそれぞれ約25人の参加者を持つと仮定しよう。SMD = 0.2 の効果を検出できるようにしたい。このようなメタ分析にはどのような検出力があるか?
# 仮定条件を定義
theta <- 0.2
K <- 10
n1 <- 25
n2 <- 25
# プール効果の標準誤差を計算
sigma <- sqrt(((n1+n2)/(n1*n2)+(theta^2/(2*n1+n2)))/K)
# z を計算
z = theta/sigma
# 検出力を計算
1 - pnorm(1.96-z) + pnorm(-1.96-z)## [1] 0.6059151このメタ分析には 10 件の研究が含まれているにもかかわらず、60.6% と検出力不足であることがわかる。固定効果メタ分析の検出力を計算するには、power.analysis 関数を使用する方が便利である。
power.analyze 関数は、以下の引数を含む。
d. 標準化平均差 (SMD) で表される仮説的な、または妥当な総合効果量。効果量は正の数値でなければならない。OR. 治療や介入の効果をコントロールと比較して想定したもので、オッズ比 (OR) で表される。dとORの両方が指定された場合、結果はdの値に対してのみ計算される。k. メタ分析に含まれると予測される研究数。n1,n2. 対象研究の第1群、第2群における平均サンプルサイズの予測値。p. 使用するアルファ値。デフォルトは \(\alpha\) = 0.05。heterogeneity. 研究間の異質性のレベル。固定効果モデルで異質性がない場合は"fixed"、異質性が低い場合は"low"、異質性が中程度の場合は"moderate"、異質性が高い場合は"high"を指定することができる。デフォルトは"fixed"。
先ほどの例と同じ入力で、この関数を試してみよう。
library(dmetar)
power.analysis(d = 0.2,
k = 10,
n1 = 25,
n2 = 25,
p = 0.05)## Fixed-effect model used.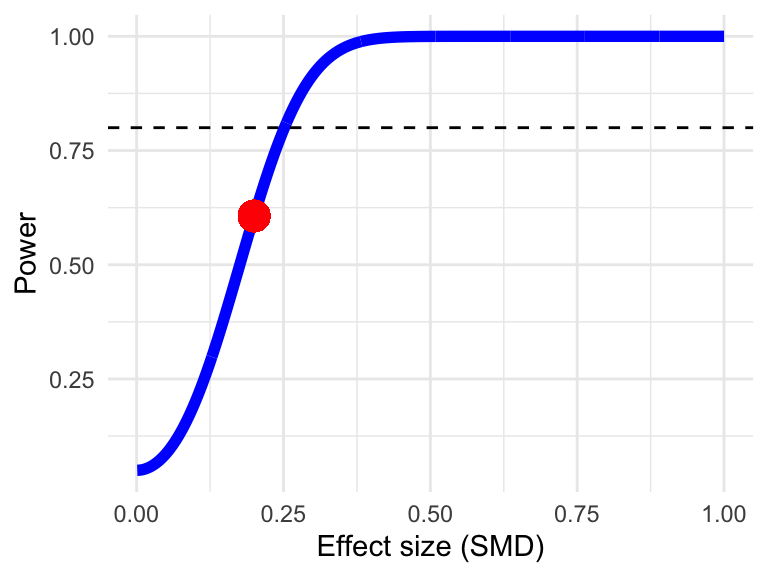
## Power: 60.66%14.2 ランダム効果モデル
ランダム効果モデルを仮定した検出力分析の場合、研究間の異質性分散 \(\tau^2\) を考慮する必要がある。したがって、標準誤差の適合版、\(\sigma^*_{\theta}\) を計算する必要がある。
\[\begin{equation} \sigma^*_{\theta}=\sqrt{\frac{\left(\frac{n_1+n_2}{n_1n_2}\right)+\left(\frac{\theta^2}{2(n_1+n_2)}\right)+\tau^2}{K}} \tag{14.5} \end{equation}\]
問題は、\(\tau^2\) の値は、通常、データを見る前にはわからないということである。しかし、Hedges and Pigott (2001) は、研究間異質性が低い、中程度、高い場合にモデル化するために使用することができるガイドラインを提供している。
低い異質性:
\[\begin{equation} \sigma^*_{\theta} = \sqrt{1.33\times\dfrac{\sigma^2_{\theta}}{K}} \tag{14.6} \end{equation}\]
中程度の異質性:
\[\begin{equation} \sigma^*_{\theta} = \sqrt{1.67\times\dfrac{\sigma^2_{\theta}}{K}} \tag{14.7} \end{equation}\]
高い異質性:
\[\begin{equation} \sigma^*_{\theta} = \sqrt{2\times\dfrac{\sigma^2_{\theta}}{K}} \tag{14.8} \end{equation}\]
また、power.analyze 関数はランダム効果メタ分析に使用することができる。異質性引数 heterogeneity を用いて、想定される研究間の異質性の大きさを制御することができる。設定可能な値は "low"、"moderate"、"high" である。前の例と同じ値を用いて、研究間の異質性が中程度の場合の期待検出力を計算してみよう。
power.analysis(d = 0.2,
k = 10,
n1 = 25,
n2 = 25,
p = 0.05,
heterogeneity = "moderate")## Random-effects model used (moderate heterogeneity assumed).
## Power: 40.76%推定された検出力は 40.76% であることがわかる。これは、標準的な 80% の閾値よりも低い値である。また、固定効果モデルを仮定した場合の 60.66% よりも低くなっている。これは、研究間の異質性がプール効果の推定値の精度を低下させ、その結果、統計的検出力が低下するためである。
Figure 14.1 は、 真の効果量、研究数、研究間の異質性の量がメタ分析の検出力に及ぼす影響を可視化している73。
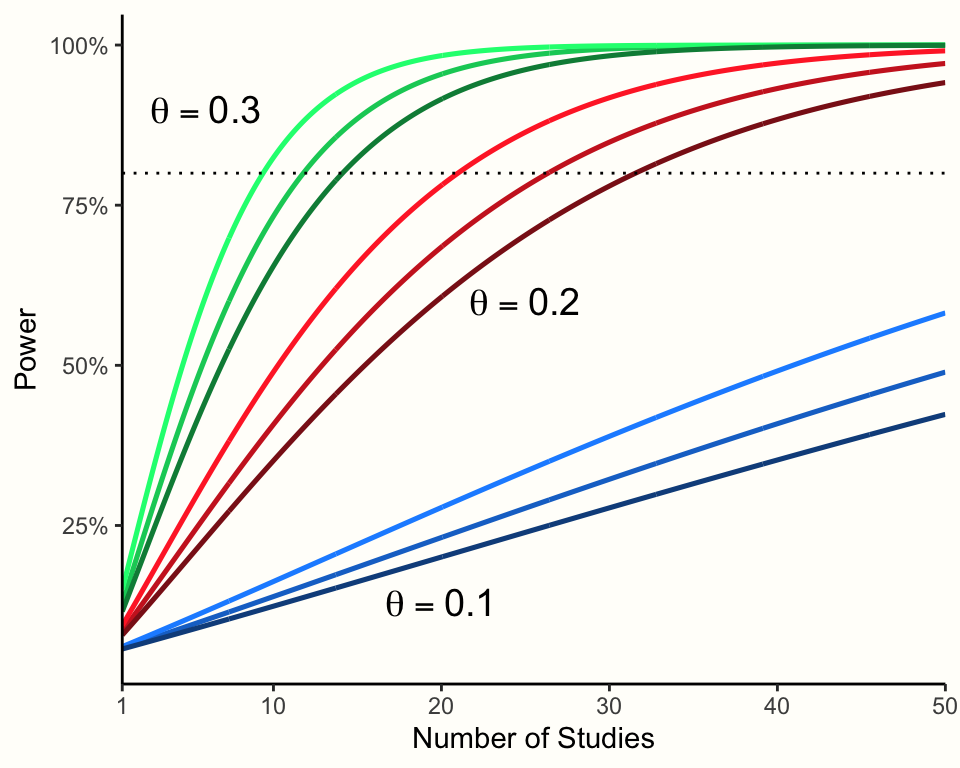
Figure 14.1: ランダム効果メタアナリシスの検出力 (各研究 \(n\)=50)。色が濃いほど、研究間の異質性が高い。
14.3 サブグループ解析
サブグループ分析を計画する際、自由に使える研究数がある場合、2 群間の差がどの程度大きければ検出できるかを知ることが重要になることがある。これは、サブグループの差のための検出力分析を適用できる条件である。 R では、Hedges and Pigott (2004) のアプローチを実装した power.analysis.subgroup 関数を用いてサブグループの検出力分析を行うことができる。
グループ 1 の効果は SMD = 0.3、標準誤差は 0.13 であり、グループ 2 の効果は SMD = 0.66、標準誤差は 0.14 であると仮定しよう。これらの仮定条件を関数の呼び出しの入力として使用することができる。
power.analysis.subgroup(TE1 = 0.30, TE2 = 0.66,
seTE1 = 0.13, seTE2 = 0.14)## Minimum effect size difference needed for sufficient power: 0.536 (input: 0.36)
## Power for subgroup difference test (two-tailed): 46.99%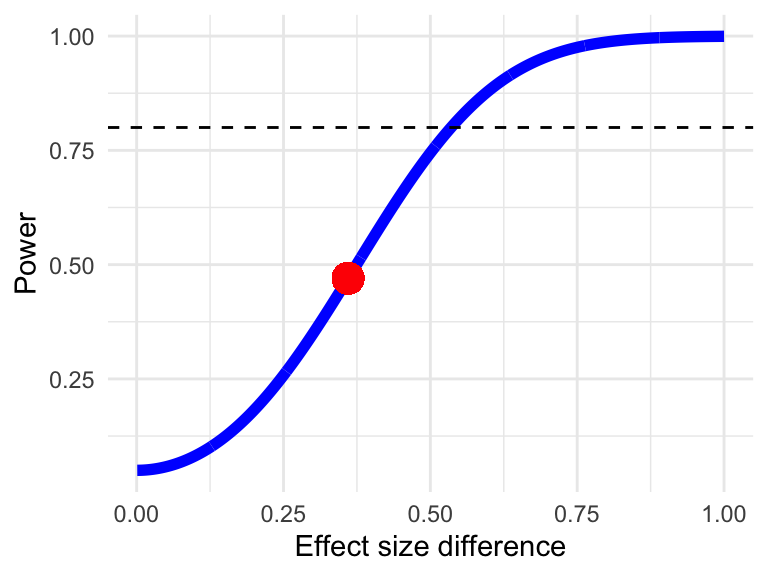
この出力では、想像上のサブグループ検定の検出力 (47%) が十分でないことがわかる。出力は、他のすべてが同じで、十分な検出力に達するには、効果量の差が少なくとも 0.54 である必要があることも教えてくれる。
\[\tag*{$\blacksquare$}\]