6 フォレストプロット

前章では、 R で効果量をプールする方法と、メタ分析で異質性を評価する方法について学んだ。ここからは、メタ分析の中でも楽しい部分で、前のステップで得た結果を可視化していく。

メタ分析を可視化する最も一般的な方法は、フォレストプロットである。このプロットは、観察された効果、信頼区間、そして通常は各研究の重み付けをグラフィカルに表示する。また、メタ分析で計算されたプール効果も表示される。全体として、この図によって、含まれる研究の精度や広がり、プール効果が観察された効果量とどのように関連しているのかを素早く調べることが可能である。

{meta} パッケージには、 R で直接美しいフォレストプロットを非常に簡単に作成するための関数が組み込まれている。この関数は幅広い機能を持ち、プロットの外観を好きなように変更することが可能である。このフォレストプロット関数と、それを実際にどのように使うことができるかが、この章の主な焦点である。さらに、メタ分析の結果を可視化するための別のアプローチについても簡単に説明する。

6.1 フォレストプロットとは？

Figure 6.1 は、フォレストプロットの主な構成要素を示している。フォレストプロットの左側には、メタ分析に含まれる各研究の名前が表示される。各研究について、通常はプロットの中央に効果量のグラフが表示され、x 軸に研究の点推定値を示している。推定値の点からは線が伸びており、観察された効果量に対して計算された信頼区間の範囲を示している。通常、点推定値は四角で囲まれている。この四角の大きさは効果量の重み (Chapter 4.1.1) で決まり、重みの大きな研究では大きな四角が、重みの小さな研究では小さな四角が与えられる。

通常、フォレストプロットにはメタ分析に使用した効果量のデータも掲載している。これにより、結果を再現するために必要なデータを他の人に提供することが可能である。

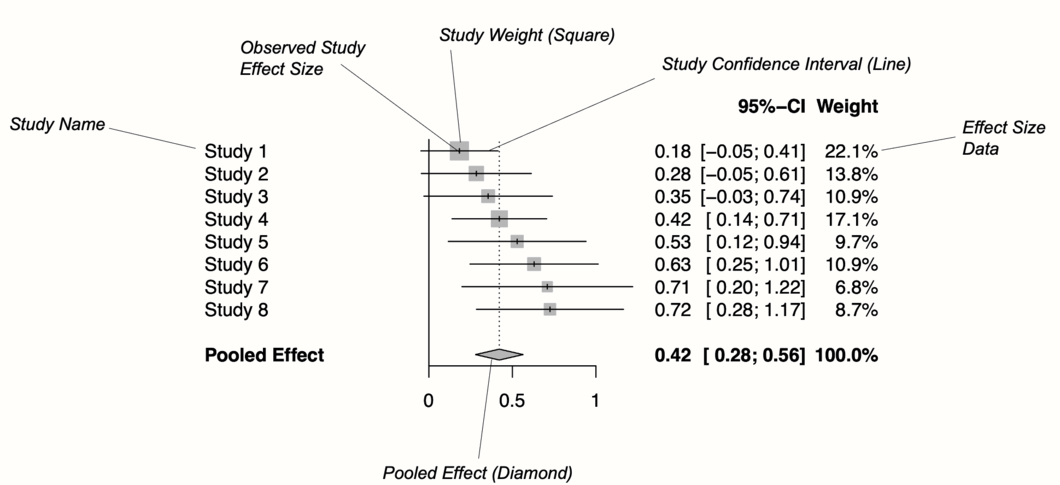
Figure 6.1: フォレストプロットの重要要素

プロットの下部にある菱形は、平均効果を表している。菱形の長さは、x 軸上のプールされた結果の信頼区間を表している。通常、フォレストプロットには垂直の参照線がある。この線は x 軸上の効果がない値を示している。さらに、フォレストプロットは、例えば、$I^2$ や $\tau^2$ のような異質性指標を表示すことによって強化されることがある。これについては、例で見ていこう。

フォレストプロットにおける効果量と信頼区間は、通常、線形スケールで表示される。しかし、要約尺度が比 (オッズ比やリスク比など) である場合、x 軸で対数スケールを使用することが一般的である。これは、1 よりずっと低い値や高い値よりも、1 付近の値の方がより多くあることを意味する。

比に意味がある効果量の測定基準は「線形」に解釈することができない (すなわち、RR = 0.50 の「反対」は 1.5 ではなく 2 である。Chapter 3.3.2 を参照)。この場合の効果量の参照線は、通常 1 であり、1 が効果がないことを示す。

6.2 R のフォレストプロット

メタ分析オブジェクト (例: metagen、metacont、metabin の結果) の種類に関わらず、 forest.meta 関数を使用してフォレストプロットを作成することが可能である (訳注: 関数名は forest でよい。一般に、 R では、 forest 関数が forest.meta のようにドット以降にクラスを指定したものを自動的に読み込む。)。forest.meta に {meta} オブジェクトを渡すだけで、プロットが作成される。通常、フォレストプロットはデフォルトで非常に良い見た目をしているが、この関数はさらに見た目を整えるための追加引数をたくさん持っている。すべての引数は関数のドキュメントに記載されている (?forest.metaを実行することでアクセス可能)。ここでは、より重要なものをリストアップしよう。

sortvar. メタ分析データセットの変数で、フォレストプロットで研究をソートするためのもの。例えば、効果量によって結果を並べ替えたい場合、sortvar = TE というコードを使用することが可能である。
comb.fixed. 論理値。固定効果モデルの推定値をプロットに含めるかどうかを示す。
comb.random. 論理値。ランダム効果モデルの推定値をプロットに含めるかどうかを示す。
text.fixed. 固定効果モデルによるプール効果のラベルを表示する。デフォルトでは "Fixed effect model" と表示される。
text.random. ランダム効果モデルによるプール効果のラベル。デフォルトでは "Random effects model" と表示される。
prediction. 論理値。予測区間をプロットに追加するかどうかを示す。
label.left と label.right. フォレストプロットの左側と右側に追加されるラベル。例えば、この側の効果は治療に有利であることを明示できる (例: label.left = "Favors treatment")。
smlab. プロットの上に表示されるラベル。どの効果量メトリックを使用したかを示すために使用できる。
xlim. x 軸の限界値、または対称的なフォレストプロットを作成したいときは文字 "s" を指定する。結果がゼロから大きく外れている場合や、外れ値を表示させたい場合に関係する。例えば、x 軸を 0 から 2 の範囲にしたい場合、コードは xlim = c(0,2) となる。
ref. プロットにおける参照線。使用した要約尺度に依存し、デフォルトでは 0 または 1 のどちらかになる。
leftcols と rightcols. ここでは、フォレストプロットの左側と右側に表示する変数を指定することができる。この関数がデフォルトで使用する要素がいくつかある。例えば、"studlab" は研究のラベル、 "effect" は観測された効果量、 effect.ci は効果量とその信頼区間を表す。また、最初に {meta} 関数に提供した data.frame に含まれていれば、ユーザー定義の列を追加することも可能である。この場合、列の名前を文字列として追加するだけである。
leftlabs と rightlabs. フォレストプロットの左側と右側に表示される列に使用されるラベル。
print.I2 と print.I2.ci. 論理値。$I^2$ 値とその信頼区間を表示すかどうかを指定する。デフォルトでは TRUE。
print.tau2 と print.tau. 論理値。$\tau^2$ と $\tau$ の値を表示すかどうかを指定する。デフォルトでは、$\tau^2$ の値を表示する。
col.square, col.diamond, col.predict. それぞれ、正方形、菱形、予測区間の色 (例: "blue") を指定する。

それではフォレストプロットを作成してみよう。この例では、前の例で使用した m.gen オブジェクトをプロットしている。フォレストプロットでは、効果量によって研究を並べ替え、予測区間を追加し、左側にユーザー定義のラベルを追加している。forest.meta 関数は、デフォルトで $\tau^2$ 値を出力するが、ここでは不要なので、print.tau2 を FALSE に設定する。

最終的にこのようなコードになる。(訳注: 原著では引数が間違っていた。pdrediction が正しい。)

forest.meta(m.gen, 
            sortvar = TE,
            prediction = TRUE, 
            print.tau2 = FALSE,
            leftlabs = c("Author", "g", "SE"))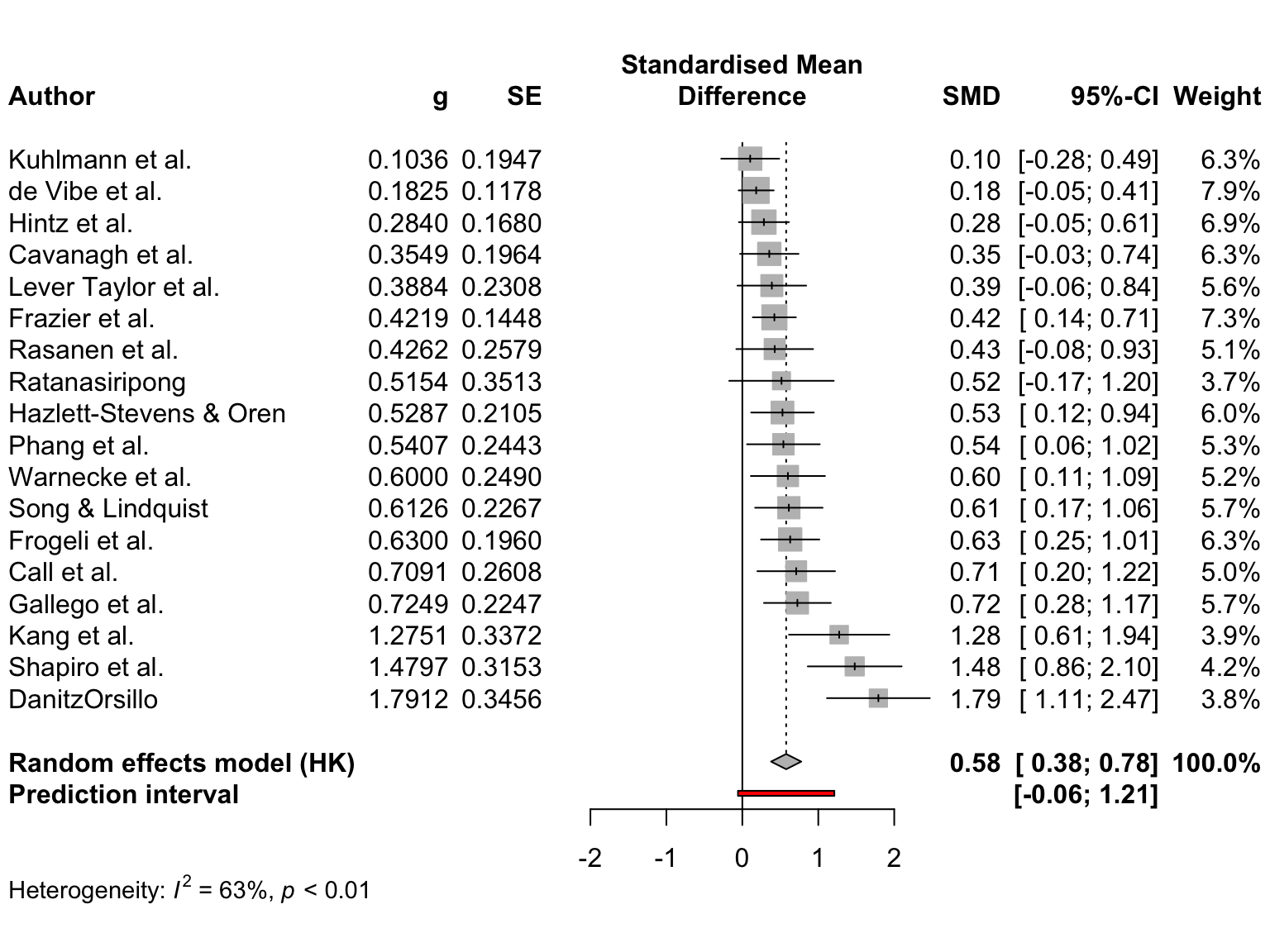

forest.meta のプロットの見た目は、すでにかなり良い。また、太めの線がプロットに追加され、プール効果の予測区間を表していることがわかる。

各研究のバイアスリスクを表示す列を追加することで、プロットを強化することが可能である。m.gen の生成に使用した ThirdWave データセットには、RiskOfBias という列があり、そこに各研究のバイアスリスク評価が保存されている。

メタ分析の計算に metagen を使用している場合 (Chapter 4.2.1)、この関数は自動的にこのデータを m.gen 内に保存する。したがって、 leftcols 引数を使用して、プロットに列を追加することが可能である。この結果、次のようなコードになる。

par(bg="#FFFEFA")
forest(m.gen, 
       sortvar = TE,
       prediction = TRUE, 
       print.tau2 = FALSE,
       leftcols = c("studlab", "TE", "seTE", "RiskOfBias"),
       leftlabs = c("Author", "g", "SE", "Risk of Bias"))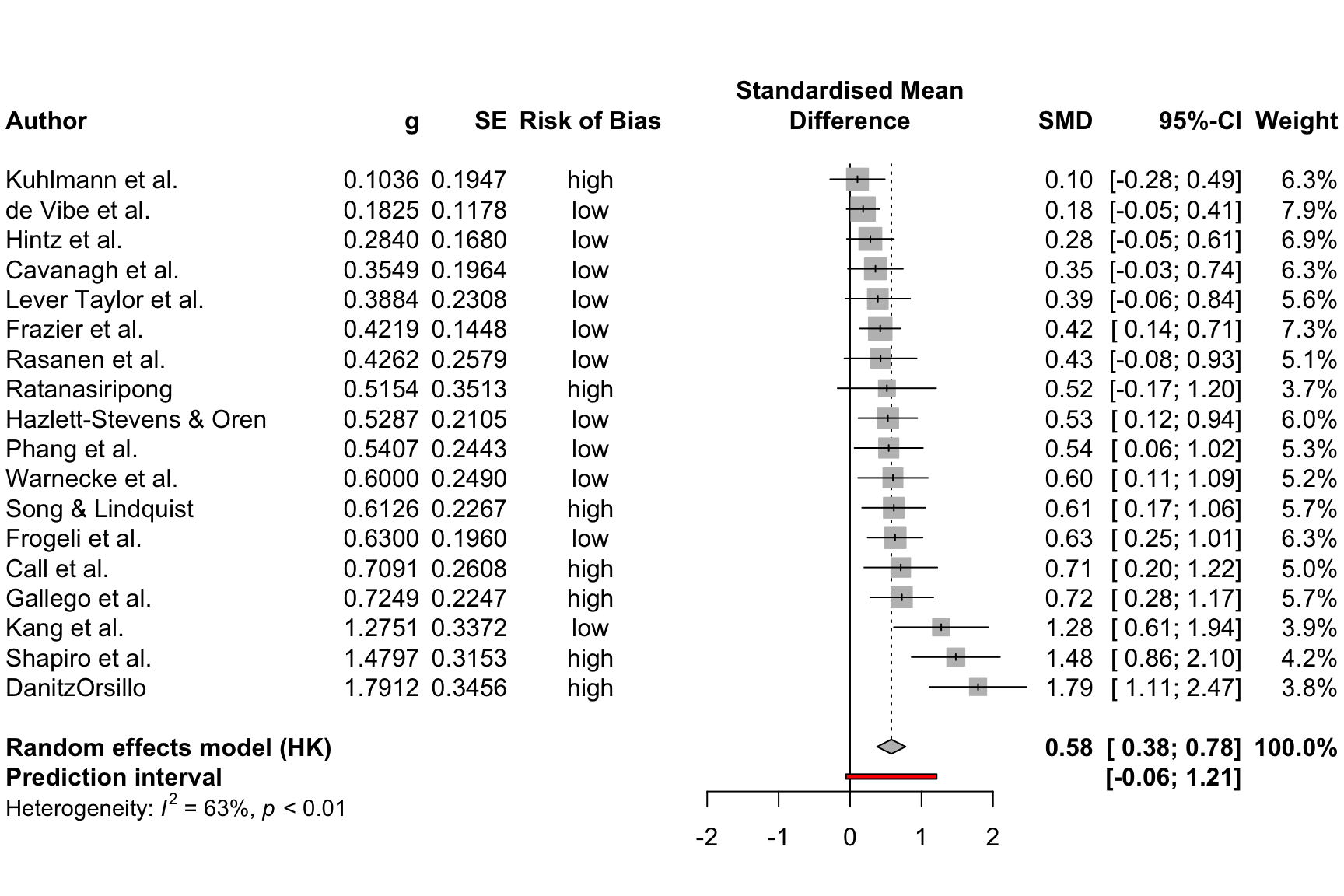

フォレストプロットに各研究のバイアスリスク情報が追加されたことがわかる。

6.2.1 レイアウトの種類

forest.meta 関数には2つの「パッケージ済み」レイアウトがあり、これを使用すると、多数の引数を指定することなくフォレストプロットを特定の形式にすることが可能である。そのうちの1つは "JAMA" レイアウトで、Journal of the American Medical Association のガイドラインに従ったフォレストプロットを提供するものである。このレイアウトは、メタ分析を医学雑誌に掲載したい場合に使用される。

forest.meta(m.gen, layout = "JAMA")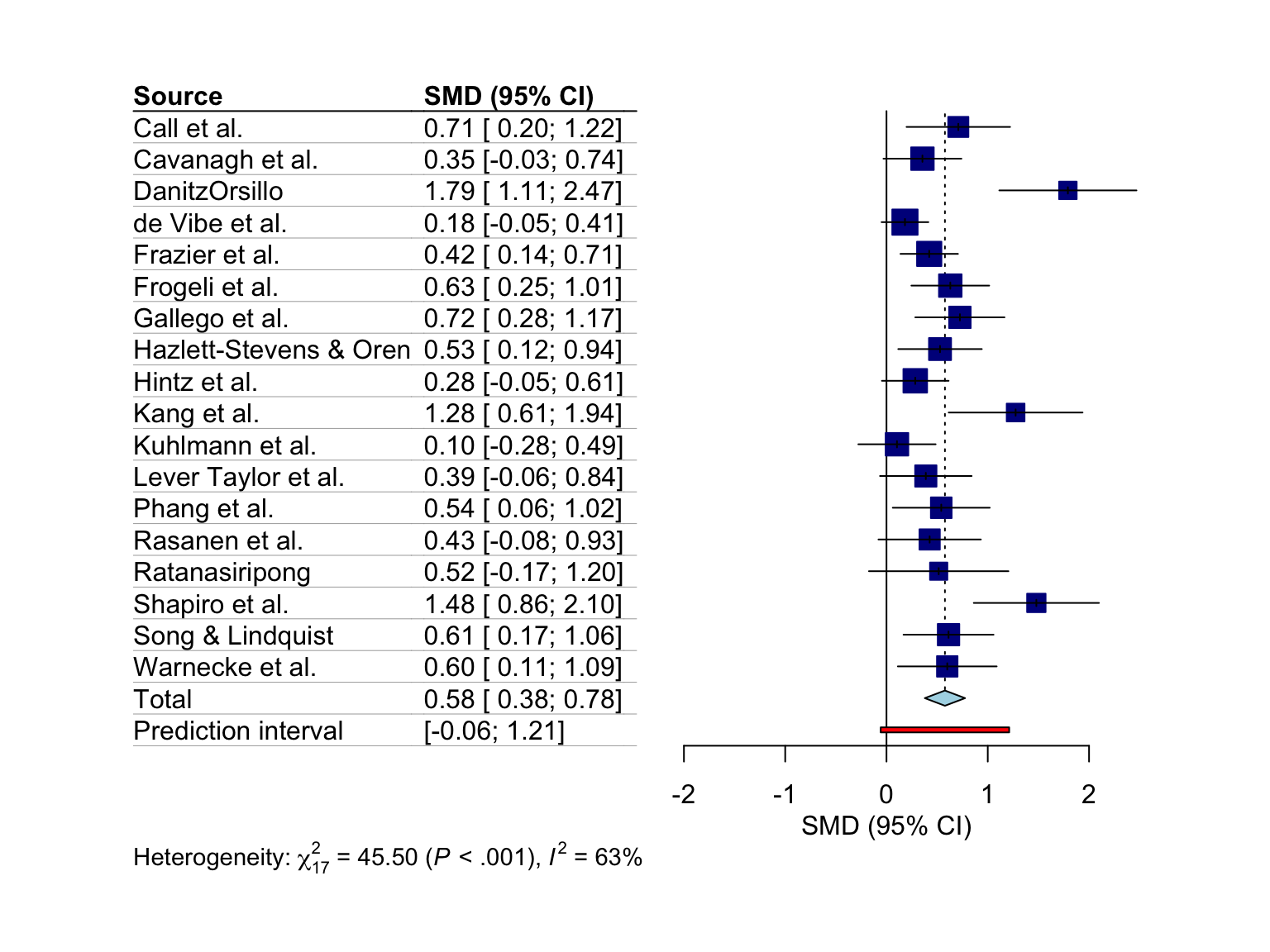

もう一つのレイアウトは "RevMan5" で、Cochrane の Review Manager 5 で生成されるものと同様のフォレストプロットを生成する。

forest.meta(m.gen, layout = "RevMan5")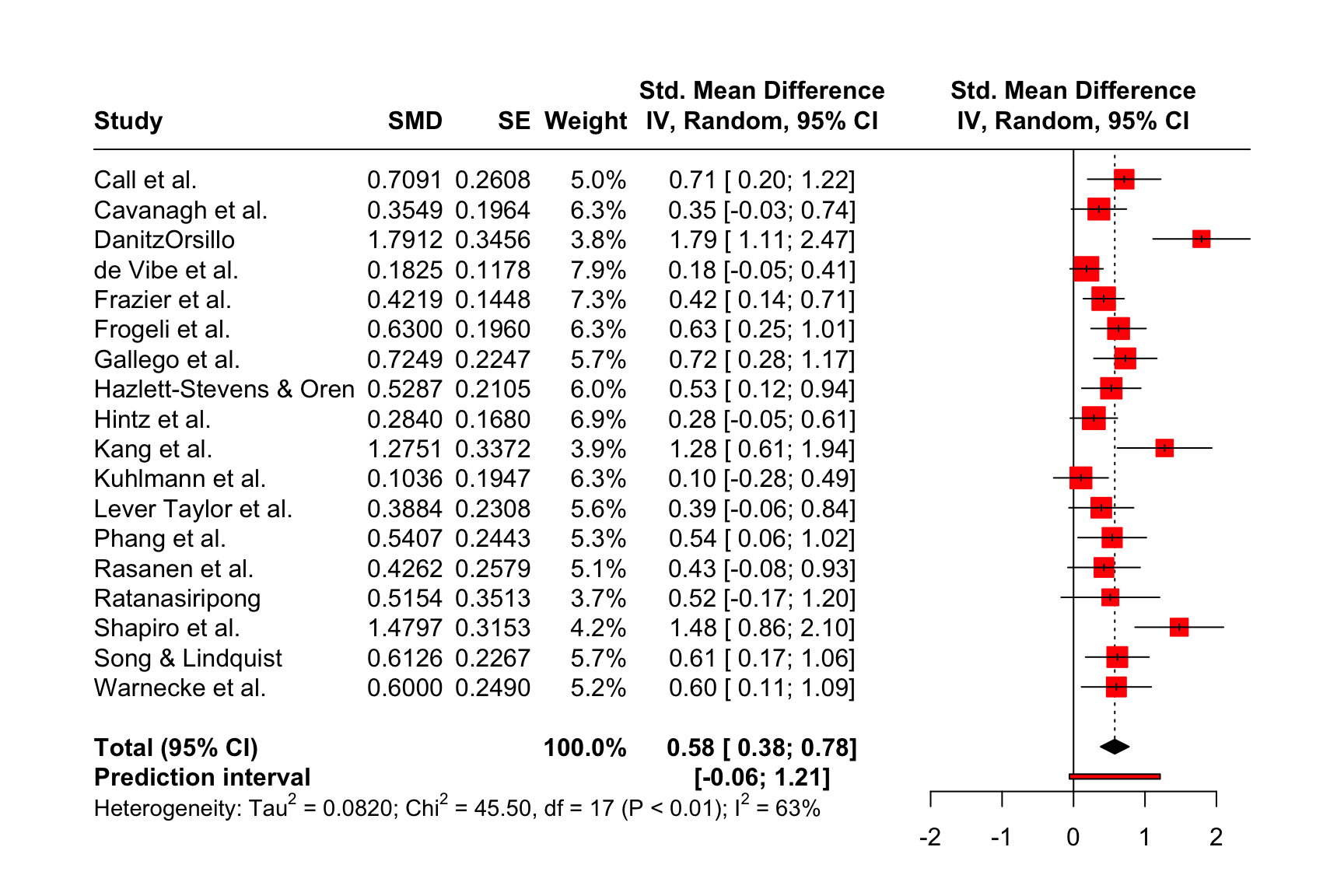

6.2.2 フォレストプロットを保存

forest.meta によって生成されたフォレストプロットは、PDF、PNG、または scalable vector graphic (SVG) ファイルとして保存することが可能である。base R や {ggplot2} パッケージによって生成される他のプロットとは対照的に、forest.meta の出力はファイルとして保存する際に自動的にサイズ調整されていない。このため、フォレストプロットは 2 辺または 4 辺が切り取られることがあり、すべてが見えるように幅と高さを手動で調整する必要がある。

pdf、png、svg 関数を使用すると、 R のコードでプロットを保存することができる。まず、いずれかの関数をコールして、次のコードの出力をドキュメントに保存するように R に指示する。そして、forest.meta 関数の呼び出しを追加する。最後の行では、dev.off() とし、生成された出力を上記で指定したファイルに保存する。

どの関数も file という引数でファイル名を指定する。ファイルは、その名前で自動的に作業ディレクトリに保存される。さらに、width と height 引数でプロットの大きさを指定することができるので、出力が途切れるような場合に役立つ。

最初のフォレストプロットを “forestplot” という名前で保存すると仮定して、以下のようなコードで PDF、PNG、SVG ファイルを生成することが可能である。

PDF

pdf(file = "forestplot.pdf", width = 8, height = 7)

forest.meta(m.gen, 
            sortvar = TE,
            prediction = TRUE, 
            print.tau2 = FALSE,
            leftlabs = c("Author", "g", "SE"))

dev.off()

PNG

png(file = "forestplot.png", width = 2800, height = 2400, res = 300)

forest.meta(m.gen, 
            sortvar = TE,
            prediction = TRUE, 
            print.tau2 = FALSE,
            leftlabs = c("Author", "g", "SE"))

dev.off()

SVG

svg(file = "forestplot.svg", width = 8, height = 7)

forest.meta(m.gen, 
            sortvar = TE,
            prediction = TRUE, 
            print.tau2 = FALSE,
            leftlabs = c("Author", "g", "SE"))

dev.off()

6.3 ドレーパリープロット

フォレストプロットは、メタ分析を可視化する最も一般的な方法である。発表されたメタ分析のほとんどにフォレストプロットが含まれており、多くの研究者がその解釈方法を理解している。フォレストプロットは、調査結果の包括的で理解しやすい要約を提供するので、メタ分析レポートにもフォレストプロットを含めることが推奨される。

しかし、フォレストプロットだけが結果を説明する手段ではない。メタ分析は、例えば、ドレーパリープロット (Rücker and Schwarzer 2021) (drapery plot、訳注: ドレーパリーとは、衣服やカーテンなどのひだのこと。美術史では、衣文とも訳される。) などでも可視化することが可能である。フォレストプロットの欠点は、固定された有意閾値、慣習的に$p<$ 0.05を仮定した信頼区間しか表示できないことである。研究者は、これらの信頼区間に基づいて、効果が有意であるか否かを決定している。

近年、$p$ 値の利用をめぐる論争があり (Wellek 2017)、$p$ 値に基づく仮説検定が、多くの研究領域で「再現性の危機」に寄与しているという議論もある (Nuzzo 2014)。

ドレーパリープロットは、$p$-値関数に基づいている。この $p$ 値関数とは、解析結果を解釈する際に $p$ < 0.05 の有意性閾値だけに頼らないために提案されたものである (Infanger and Schmidt-Trucksäss 2019)。

したがって、$p$ 値関数は 95% 信頼区間を計算するだけでなく、$p$ の値を変化させた場合の信頼区間を示す連続曲線を提供する。ドレーパリープロットでは、各研究の信頼曲線と平均効果の信頼曲線がプロットされる。x 軸は効果量指標を示し、y 軸は仮定された $p$ 値を示す。

ドレーパリープロットは、 {meta} の drapery 関数によって生成することが可能である。forest.meta と同様に、この関数に {meta} メタ分析オブジェクトを与えると、自動的にプロットが生成される。追加引数が複数あるが、最も重要なのは以下の引数である。

type: y 軸にプロットされる値の種類を定義する。検定統計量の "zvalue" (デフォルト)、または $p$-値 ("pvalue") とする。
study.results: 論理値。各研究の結果をプロットに含めるかどうかを指定する。FALSE の場合、効果の要約のみが表示される。
labels: この引数を "studlab" に設定すると、試験のラベルがプロットに含まれるようになる。
legend: 論理値。凡例を表示すかどうかを示す。
pos.legend. 凡例の位置。"bottomright"、"bottom"、"bottomleft"、"left"、"topleft"、"top"、"topright"、"right"、"center" のいずれかを指定。

メタ分析オブジェクト m.gen を使って drapery 関数を試してみよう。

drapery(m.gen, 
        labels = "studlab",
        type = "pval", 
        legend = FALSE)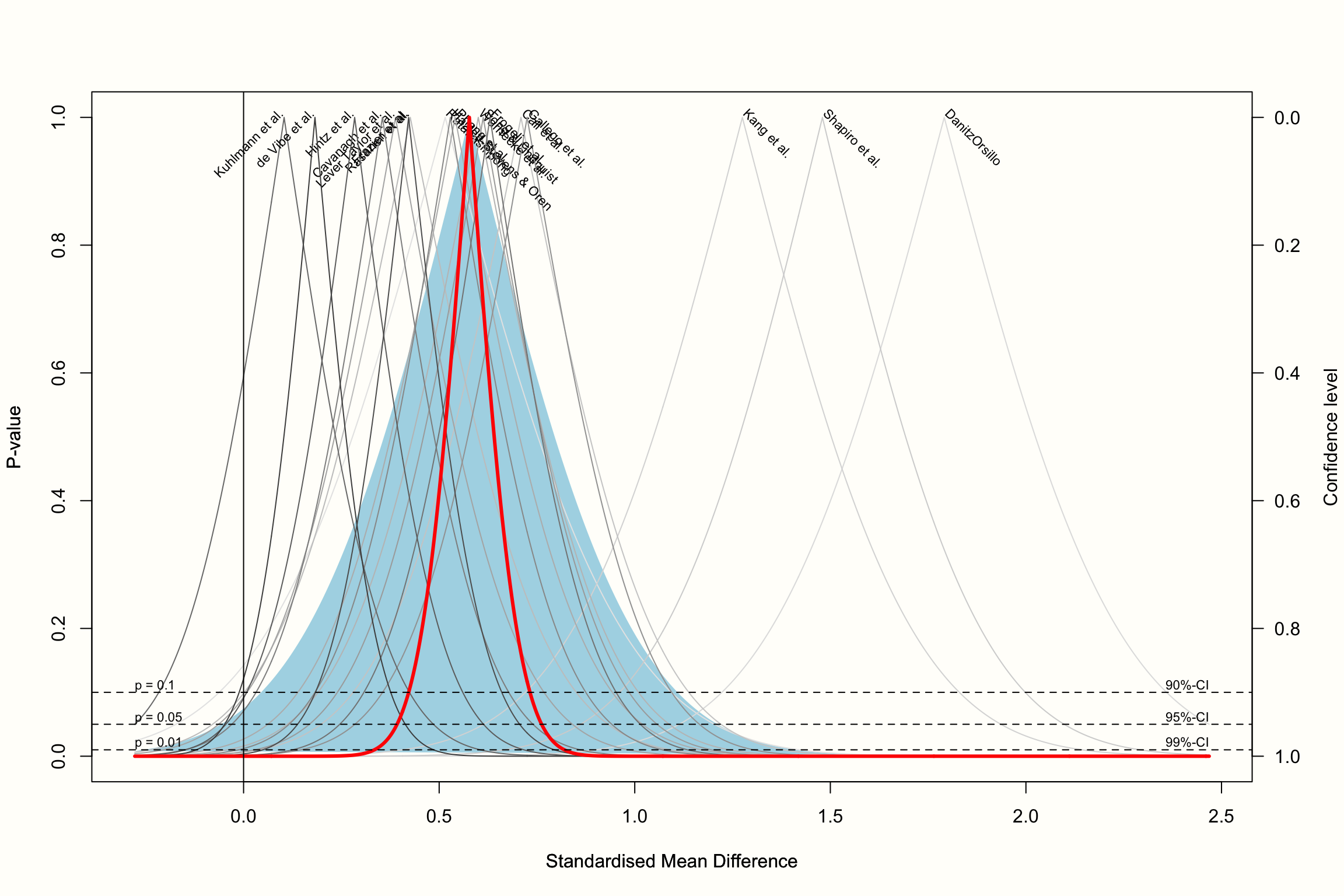

結果として得られるプロットは、各効果量の $p$-値曲線を含み、すべて逆 V 字の形をしている。太線はランダム効果モデルによる平均効果を表した。プロットで見られる斜線部分は予測区間で、プール効果の信頼区間よりもかなり広い。

$p$ 値関数の「ピーク」は、メタ分析における効果量の正確な値を表している。y 軸を下に行くに従って、$p$ 値は小さくなり、信頼区間は広くなり、破線の水平線で示される従来の有意閾値に到達することになる。

$p$ がすでに非常に小さいとき (<0.01) に太線が x 軸上でゼロになることから、プロットに基づいて、プール効果量がゼロより大きいことをかなり確信できることがわかる。

Rücker et al. (2021) は、ドレーパリープロットは主にフォレストプロットに加えて使用すべきであると推奨している。なぜなら、フォレストプロットは、結果を再現するために必要な効果量情報を含んでいないことがある。

\[\tag*{$\blacksquare$}\]

6.4 演習問題

知識を試そう！

フォレストプロットの主要な構成要素は何か？

メタ分析でフォレストプロットを提示するメリットは何か？

フォレストプロットの限界は何か、ドレーパリープロットはこの限界をどのように克服しているのか。

問題の解答は、本書の巻末 Appendix A にある。

6.5 要約

メタ分析の結果は、フォレストプロットで可視化するのが一般的である。
フォレストプロットは、各研究の効果量と信頼区間をグラフ化したもので、総合効果の計算値も表示される。さらに、プールに使用された効果量データも含まれる。
フォレストプロットには、各研究が受けた品質評価など、他の種類の情報を追加することも可能である。

5 研究間異質性

7 サブグループ解析